Desigualdad de las medias aritmética y geométrica

Desigualdad de las medias aritmética y geométrica: Desigualdad de las medias aritmética y geométrica

Saltar a navegación, búsqueda

Contenido

1 Desigualdad de las medias aritmética y geométrica

2 Media aritmética y media geométrica

3 La desigualdad

4 Demostración por inducción

5 Véase también

6 Referencias

Desigualdad de las medias aritmética y geométrica

En matemáticas, se conoce como desigualdad entre media aritmética y geométrica, o MA-MG, aquella desigualdad que establece que la media aritmética de un conjunto de números reales positivos es mayor o igual que la media geométrica del mismo conjunto, cumpliéndose únicamente la desigualdad cuando todos los elementos del conjunto sean iguales.

Media aritmética y media geométrica

La media aritmetica de un conjunto 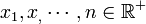${x_1,x_,\cdots ,n}\in\mathbb R^+$ , es igual a la suma dividida por el número total de elementos,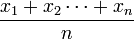

$\frac{x_1+x_2\cdots+x_n}{n}$

La media geométrica de un conjunto 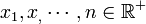${x_1,x_,\cdots ,n}\in\mathbb R^+$ , es igual a la raíz n-ésima del producto de todos ellos.

$\sqrt[n]{x_1x_2 \cdots x_n}$

La desigualdad

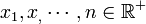Sea ${x_1,x_,\cdots ,n}\in\mathbb R^+$ ,

$\frac{x_1+x_2\cdots+x_n}{n}\geq\sqrt[n]{x_1x_2 \cdots x_n}$

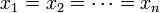
Cumpliendose la igualdad si y sólo si ${x_1 = x_2 = \cdots = x_n}$

$\frac{x_1+x_2\cdots+x_n}{n}=\sqrt[n]{x_1 x_2 \cdots x_n}$

Demostración por inducción

Para demostrar la desigualdad MA-MG, se desarrollara por el metodo de inducción matemática, demostrando que la MA-MG es cierta para 2 elementos, luego generalizandolo para 2n elementos y demostrando que si cierta para n es cierta para n+1 elementos.

Sea 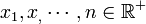${x_1,x_,\cdots ,n}\in\mathbb R^+$ , un conjunto de n elementos ,

Procedemos a considerar el primer paso en que n=2

$\frac{x_1 + x_2 }{2}\geq\sqrt[2]{x_1 x_2}$

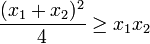
$\frac{(x_1 + x_2)^2 }{4}\ge x_1 x_2$

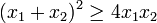
$(x_1 + x_2)^2 \ge 4x_1 x_2$

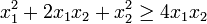
$x_1^2+2x_1x_2+x_2^2 \ge 4x_1 x_2$

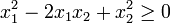
$x_1^2-2x_1x_2+x_2^2 \ge 0$

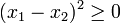
$(x_1-x_2)^2\ge0$

Quedando asi demostrado para n=2, luego se demuestra que si cierta para 2 es cierta para 2n elementos.

$\frac{x_1+x_2\cdots+x_{2n}}{2n}\geq\sqrt[2n]{x_1 x_2 \cdots x_{2n}}$

$\frac{\frac{(x_1+x_2+\cdots+x_{n+1})}{n}+\frac{(x_{n+1}+x_{n+2}+\cdots+x_{2n})}{n}}{2}\ge \sqrt[2]{\frac{(x_1+x_2+\cdots+x_{n+1})}{n}\frac{(x_{n+1}+x_{n+2}+\cdots+x_{2n})}{n}}$

Suiguiendo la hipótesis,

$\frac{x_1+x_2\cdots+x_n}{n}\geq\sqrt[n]{x_1 x_2 \cdots x_n}$

Se sigue que,

$\frac{\frac{(x_1+x_2+\cdots+x_{n+1})}{n}+\frac{(x_{n+1}+x_{n+2}+\cdots+x_{2n})}{n}}{2}\ge \sqrt[2]{\sqrt[n]{(x_1x_2\cdots x_{n+1})} \sqrt[n]{(x_{n+1}x_{n+2}\cdots x_{2n})}}$

Siendo esto igual a,

$\frac{x_1+x_2\cdots+x_{2n}}{2n}\geq\sqrt[2n]{x_1 x_2 \cdots x_{2n}}$

Quedando asi demostrado que si es cierto para 2 elementos es cierto para 2n elementos.

Ahora procedemos a demostrar que si es cierta para n elementos es cierta para n-1 elementos,

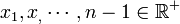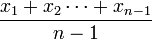
Sea ${x_1,x_,\cdots ,{n-1}}\in\mathbb R^+$ y $\frac{x_1+x_2\cdots+x_{n-1}}{n-1}$

Se considera la desigualdad de todos los emlementos mencionados,

$\frac{x_1+x_2+\cdots x_{n-1} +\frac{x_1+x_2\cdots+x_{n-1}}{n-1}}{n}\geq\sqrt[n]{x_1x_2\cdots x_{n-1}\frac{x_1+x_2\cdots+x_{n-1}}{n-1}}$

$\frac{(n-1)x_1+(n-1)x_2+\cdots +(n-1)x_{n-1} +x_1+x_2\cdots+x_{n-1}}{(n-1)n}\geq\sqrt[n]{x_1x_2\cdots x_{n-1}}\sqrt[n]{\frac{x_1+x_2\cdots+x_{n-1}}{n-1}}$

$\frac{nx_1+nx_2+\cdots +nx_{n-1}}{(n-1)n}\geq\sqrt[n]{x_1x_2\cdots x_{n-1}}\sqrt[n]{\frac{x_1+x_2\cdots+x_{n-1}}{n-1}}$

$\frac{x_1+x_2+\cdots +x_{n-1}}{n-1}\geq\sqrt[n]{x_1x_2\cdots x_{n-1}}\sqrt[n]{\frac{x_1+x_2\cdots+x_{n-1}}{n-1}}$

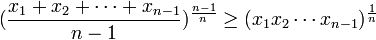
$(\frac{x_1+x_2+\cdots +x_{n-1}}{n-1})^\frac{n-1}{n}\geq ({x_1x_2\cdots x_{n-1}})^{\frac{1}{n}}$

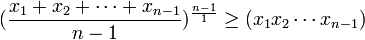
$(\frac{x_1+x_2+\cdots +x_{n-1}}{n-1})^\frac{n-1}{1}\geq ({x_1x_2\cdots x_{n-1}})$

Haciendo raíz n-1-ésima se sigue,

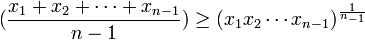
$(\frac{x_1+x_2+\cdots +x_{n-1}}{n-1})\geq ({x_1x_2\cdots x_{n-1}})^\frac{1}{^n-1}$

Quedando asi demostrado por el metodo inductivo, la veracidad de la desigualdad MA-MG.

$\frac{x_1+x_2\cdots+x_n}{n}\geq\sqrt[n]{x_1 x_2 \cdots x_n} , \forall n \in\mathbb N$ Q.E.D.

Véase también

Inecuación

Desigualdad

Media aritmética

Media geometrica

Inducción matemática

Referencias

Oleksandr, karlein.Rondero Guerrero, Carlos.Tarasenko, Anna. (2008). Desigualdades, métodos de calculo no tradicionales". Díaz de Santos. ISBN 978-84-7978-807-0

Obtenido de "Desigualdad de las medias aritm%C3%A9tica y geom%C3%A9trica"

Categorías: Desigualdades | Medias

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Parámetro estadístico — Saltar a navegación, búsqueda La media aritmética … Wikipedia Español
Thomas Malthus — Thomas Robert Malthus Nacimiento … Wikipedia Español

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos