Inecuación

Inecuación
 Se ha sugerido que este artículo o sección sea fusionado en Desigualdad matemática (discusión).
Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí.

"Menor que" y "Mayor que" redirigen aquí. Para el uso de "<" y ">" como signos de puntuación véase Paréntesis.

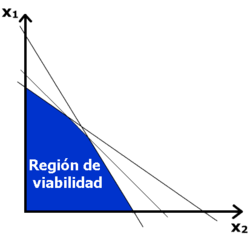La región de viabilidad en un problema de programación lineal está definida por un juego de inecuaciones.

Una inecuación es una expresión matemática la cual se caracteriza por tener los signos de desigualdad. Siendo una expresión algebraica nos da como resultado un conjunto en el cual la variable independiente puede tomar el valor cualquiera de ese conjunto cumpliendo esta desigualdad. A este conjunto se le conoce como intervalo. Una de las obligaciones de las (inecuaciones) es la de cumplir una desigualdad

En matemáticas, una inecuación es una expresión referida al tamaño u orden relativo de dos objetos (ver también ecuación). La notación a < b significa que a es menor que b y la notación a > b quiere decir que a es mayor que b. Estas relaciones son conocidas con el nombre de inecuaciones estrictas, contrastando con a ≤ b (a es menor o igual a b) y a ≥ b (a es mayor o igual que b), llamadas inecuaciones no estrictas.

Si el signo comparativo de la inecuación es el mismo para cualquier valor que tomen las variables por las que está definida, entonces se hablará de una inecuación "absoluta" o "incondicional" (véase identidad).

Si por el contrario, el signo comparativo es el mismo sólo para ciertos valores de las variables, pero se invierte o cambia para otros valores, será una inecuación "condicional".

El signo comparativo de una inecuación no se cambia si a ambos miembros se les suma o resta el mismo número real, o si se les multiplica o divide por un número positivo; en cambio, se invierte si a ambos miembros se les multiplica o divide por un número negativo.

La notación a >> b quiere decir que a "es mucho mayor que" b. El significado de esto puede variar, refiriéndose a una diferencia entre ambos indefinida. Se usa en ecuaciones en las cuales un valor mucho mayor causará que la resolución de la ecuación arroje a luz un cierto resultado.

Contenido

Propiedades

Las inecuaciones se rigen por las siguientes propiedades:

Tricotomía

La propiedad de la tricotomía dicta que, para dos números reales cualesquiera a y b, sólo se cumplirá una de las siguientes propiedades:

  • \, a < b
  • \, a = b
  • \, a > b

Simetría

Las relaciones en inecuaciones pueden ser invertidas, queriendo decir esto que:

  • Para dos números reales, a y b:
    • Si   \, a > b   entonces   \, b < a
    • Si   \, a < b   entonces   \, b > a

Transitiva

  • Para tres números reales, a, b y c:
    • Si   \, a > b   y   \, b > c   entonces   \, a > c
    • Si   \, a < b   y   \, b < c   entonces   \, a < c
    • Si   \, a > b   y   \, b = c   entonces   \, a > c
    • Si   \, a < b   y   \, b = c   entonces   \, a < c

Adición y sustracción

Si a los dos miembros de una desigualdad se suma o resta una misma cantidad, el signo de la cantidad no varia.

  • Para tres números reales, a, b, y c:
    • Si   \, a > b   ; entonces \, a + c > b + c   y   \, a - c > b - c
    • Si   \, a < b   ; entonces \, a + c < b + c   y   \, a - c < b - c

Multiplicación y división

Las propiedades relativas a la multiplicación y la división:

  • Para tres números reales, a, b, y c:
    • Si \, c es positivo   y   \, a > b   entonces   \, a \times c > b \times c   y   \, \frac{a}{c} > \frac{b}{c}
    • Si \, c es positivo   y   \, a < b   entonces   \, a \times c < b \times c   y   \, \frac{a}{c} < \frac{b}{c}
    • Si \, c es negativo   y   \, a > b   entonces   \, a \times c < b \times c   y   \, \frac{a}{c} < \frac{b}{c}
    • Si \, c es negativo   y   \, a < b   entonces   \, a \times c > b \times c   y   \, \frac{a}{c} > \frac{b}{c}

Nota:

Si ambos términos de una inecuación se multiplican o dividen por la misma expresión negativa, el símbolo de la desigualdad CAMBIA.pero siempre hay que tener en cuenta que el resultado debe cumplir la condicion dada.

Aplicando una función a ambos miembros

Puede aplicarse cualquier función monótona creciente a ambos lados de una inecuación manteniendo el mismo signo de desigualdad.

Valor absoluto o módulo

  • |a| \le b \iff -b \le a \le b
  • |a| \ge b \iff a \ge b \vee a \le -b

Notación encadenada

La notación a < b < c establece que a < b (a menor que b) y que b < c (b menor que c) y aplicando la propiedad transitiva anteriormente citada, puede deducirse que a < c (a menor que c). Obviamente, aplicando las leyes anteriores, puede sumarse o restarse el mismo número real a los tres términos, así como multiplicarlos o dividirlos todos por el mismo número (distinto de cero) invirtiendo las inecuaciones según su signo. Debe tenerse cuidado de utilizar en todos los casos el mismo número. Así, a < b + e < c es equivalente a a - e < b < c - e.

Esta notación se puede extender a cualquier número de términos: por ejemplo, a1 ≤ a2 ≤ ... ≤ an establece que ai ≤ ai+1 para i = 1, 2, ..., n−1. Según la propiedad transitiva, esta condición es equivalente a ai ≤ aj para cualesquiera 1 ≤ i ≤ j ≤ n.

Ocasionalmente, la notación encadenada se usa con inecuaciones en diferentes direcciones. En ese caso el significado es la conjunción lógica de las desigualdades entre los términos adyacentes. Por ejemplo, a < b > c ≤ d significa que a < b, b > c, y c ≤ d. Aparte del uso poco frecuente en matemáticas, esta notación existe en unos pocos lenguajes de programación tales como Python.

Véase también

Referencias

  • Hardy, G., Littlewood J.E., Polya, G. (1999). Inequalities, Cambridge Mathematical Library, Cambridge University Press. ISBN 0521052068.
  • Beckenbach, E.F., Bellman, R. (1975). Introduction to Inequalities, Random House Inc. ISBN 0394015592.
  • Drachman, Byron C., Cloud, Michael J. (1998). Inequalities: With Applications to Engineering, Springer-Verlag. ISBN 0387984046.
  • Baldor, Aurelio. (1975) "Algebra", Edime organiacion grafica s.a. Madrid. ISBN 84-399-0259-x

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • inecuación — sustantivo femenino 1. Área: matemáticas Desigualdad algebraica en la que aparecen una o más incógnitas y que se verifica para ciertos valores que a ellas se den …   Diccionario Salamanca de la Lengua Española

  • Inecuación — ► sustantivo femenino MATEMÁTICAS Desigualdad entre dos expresiones algebraicas de una o varias variables, que sólo se verifica para ciertos valores de estas variables. * * * inecuación f. Mat. Desigualdad con una o más incógnitas. * * * Una… …   Enciclopedia Universal

  • inecuación — {{＃}}{{LM I21679}}{{〓}} {{［}}inecuación{{］}} ‹i·ne·cua·ción› {{《}}▍ s.f.{{》}} Desigualdad matemática entre unas cantidades conocidas y otras desconocidas o incógnitas: • La expresión ‘5x 5 > 0’ es una inecuación.{{○}} …   Diccionario de uso del español actual con sinónimos y antónimos

  • Fórmula autorreferente de Tupper — La fórmula autorreferente de Tupper es una fórmula autorreferente diseñada por Jeff Tupper, la cual, representada en dos dimensiones, se reproduce ella misma visualmente. Se usa en diversos cursos de matemáticas e informática como ejercicio de… …   Wikipedia Español

  • Polos y ceros — Saltar a navegación, búsqueda En matemáticas polos y ceros es un método que permite evaluar los polos y los ceros de las expresiones racionales para hallar el conjunto solución en desigualdades. Su utilidad radica en la generalización y… …   Wikipedia Español

  • Ley de Grashof — La Ley de Grashof establece que un mecanismo de cuatro barras tiene al menos una articulación de revolución completa, si y solo si la suma de las longitudes de la barra más corta y la barra más larga es menor o igual que la suma de las longitudes …   Wikipedia Español

  • Límite de una función — El límite de una función es un concepto fundamental del cálculo diferencial matemático, un caso de límite aplicado a las funciones. Informalmente, el hecho que una función f tiene un límite L en el punto c, significa que el valor de f puede ser… …   Wikipedia Español

  • Superaditividad — En matemáticas, una secuencia { an }, n ≥ 1, es llamada superaditiva si satisface la siguiente inecuación para todo valor de m y n: Contenido 1 Lema de Fekete 2 Superaditividad en funciones …   Wikipedia Español

  • Número de Dedekind — …   Wikipedia Español

  • Formulación débil de una ecuación diferencial — La formulación débil (o formulación variacional) de un problema definido mediante ecuaciones diferenciales es una forma alternativa en que dichas ecuaciones se escriben en forma integral, dando lugar a ecuaciones tratables mediante los métodos… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”