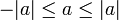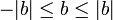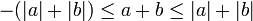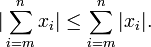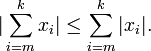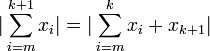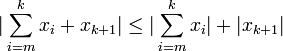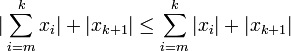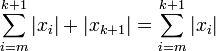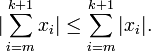Desigualdad triangular

Desigualdad triangular

Desigualdad triangular

Desigualdad del triángulo

El teorema de desigualdad triangular afirma que en cualquier triángulo la longitud de uno de los lados no puede nunca superar a la suma de las longitudes de los otros dos.

Contenido

Espacios vectoriales normados

El teorema puede generalizarse a espacios vectoriales normados, obteniéndose la siguiente versión de la desigualdad triangular:

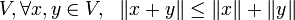
En todo espacio vectorial normado V, \forall x,y\in V, \ \ \left\| x + y \right\| \leq \left\| x \right\| + \left\| y \right\|

Es decir, que La norma de la suma de dos vectores es siempre menor o igual a la suma de las normas de los dos vectores.

En el caso particular de considerar la recta real como espacio vectorial normado con el valor absoluto como norma obtenemos la siguiente versión del teorema:

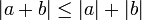
Para cualquiera dos números a y b, |a + b| \le |a| + |b|

cuya demostración es:

Demostración (caso real)

Haciendo uso de las propiedades del valor absoluto, es posible escribir:

-|a| \le a \le |a|
-|b| \le b \le |b|

Sumando ambas inecuaciones:

-(|a| + |b|) \le a + b \le |a| + |b|

A su vez, usando la propiedad de valor absoluto 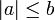|a| \le b si y solo si 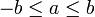-b \le a \le b en la línea de arriba queda:

|a + b| \le |a| + |b|

Desigualdad triangular para un espacio n-dimensional

Está dada por la expresión:

|\sum_{i=m}^n x_i| \le \sum_{i=m}^n |x_i|.

donde m y n son números naturales, y xi números reales.

Demostración

Ahora vamos a demostrar que la expresión anterior es cierta para cualquier n natural utilizando el método de Inducción matemática. ( Supondremos que para n=2 ya está demostrado en inicio del artículo)

1) Para n=1:

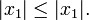|x_1| \le |x_1|. (si bien son iguales, es cierto que un número es menor o igual a sí mismo)

2) Ahora asumimos que se cumple para n=k, con k un número natural mayor que uno.

|\sum_{i=m}^k x_i| \le \sum_{i=m}^k |x_i|.
  • y probamos que la desigualdad también se cumple para n=k+1.

Partimos de la siguiente expresión:

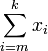|\sum_{i=m}^{k+1} x_i| = |\sum_{i=m}^k x_i + x_{k+1} |
  • como \sum_{i=m}^k x_i es un número y xk + 1 es otro, podemos aplicar la desigualdad triangular para n=2
|\sum_{i=m}^k x_i + x_{k+1} | \le |\sum_{i=m}^k x_i | + | x_{k+1} |
  • luego, como | xk + 1 | es siempre positivo y hemos asumido que se cumple para n=k podemos afirmar que:
|\sum_{i=m}^k x_i | + | x_{k+1} | \le \sum_{i=m}^k | x_i | + | x_{k+1} |
  • juntando el termino k+1 con la sumatoria nos queda:
\sum_{i=m}^{k+1} | x_i | + | x_{k+1} | = \sum_{i=m}^{k+1} | x_i |
  • Partimos de 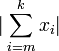|\sum_{i=m}^k x_i|, nos movimos mediante pasos lícitos por igualdades y desigualdades del tipo "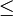\le" hasta llegar a 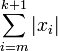\sum_{i=m}^{k+1} |x_i|, por lo que podemos concluir que:
|\sum_{i=m}^{k+1} x_i| \le \sum_{i=m}^{k+1} |x_i|.

Véase también

Obtenido de "Desigualdad triangular"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Desigualdad triangular — Nota: No debe confundirse con la Desigualdad del triángulo La propiedad de la desigualdad triangular afirma que: <blockquote style= padding: 1em; border: 2px dotted purple; > Dados dos números reales a y b, se cumple que Haciendo uso de las… …   Enciclopedia Universal

  • Desigualdad de Minkowski — Saltar a navegación, búsqueda En analisis matematico, la desigualdad de Minkowski establece que los espacios Lp son espacios vectoriales con una norma. Sea S un espacio medible, sea 1 ≤ p ≤ ∞ y sea f y g elementos de Lp(S). Entonces f + g es de… …   Wikipedia Español

  • desigualdad — ► sustantivo femenino 1 Calidad de desigual. ANTÓNIMO igualdad 2 Aspereza de un terreno o de la superficie de un cuerpo o un objeto. 3 MATEMÁTICAS Expresión algebraica que expresa la falta de igualdad entre dos cantidades. * * * desigualdad f.… …   Enciclopedia Universal

  • Desigualdad del triángulo — Nota: No debe confundirse con la Desigualdad triangular En matemáticas, la desigualdad del triángulo es un teorema que dice, aproximadamente, que el viaje de á á nunca es más corto que el viaje de á . Aplica en espacios como el de números reales …   Enciclopedia Universal

  • Espacio métrico — Saltar a navegación, búsqueda En matemática, un espacio métrico es un tipo particular de espacio topológico donde una distancia entre puntos está definida. Corresponde al caso muy común en que se dispone de una noción de distancia sobre el… …   Wikipedia Español

  • Fórmula de Herón — Triángulo de lados a, b, c. En geometría, la fórmula de Herón, descubierta por Herón de Alejandría, relaciona el área de un triángulo en términos de las longitudes de sus lados a, b y c …   Wikipedia Español

  • Norma vectorial — Un vector es un elemento de un espacio vectorial del que, en ocasiones, especialmente en Física y Geometría, interesa conocer su longitud. Para ello se hace necesario definir un operador norma que determine la longitud o magnitud del vector bajo… …   Wikipedia Español

  • Espacio prehilbertiano — Saltar a navegación, búsqueda En matemáticas, un espacio prehilbertiano o espacio prehilbert es un espacio vectorial provisto de un producto escalar. Más concretamente, es un par , donde es un espacio vectorial sobre un cuerpo y …   Wikipedia Español

  • Valor absoluto — En matemática, el valor absoluto o módulo[1] de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo ( ). Así, por ejemplo, 3 es el valor absoluto de 3 y de 3. El valor absoluto está relacionado con… …   Wikipedia Español

  • Convergencia — Saltar a navegación, búsqueda Para otros usos de este término, véase convergencia (desambiguación). En análisis matemático, el concepto de convergencia hace referencia a la propiedad que poseen algunas sucesiones numéricas de tender a un límite.… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”