- Diagrama de estados
-
Diagrama de estados
si representamos una substancia en un gráfico su presión de vapor para cada temperatura(marcados en el gráfico como líneas gruesas y continuas) y añadimos la temperatura del cambio de estado (marcados como líneas más delgadas y discontinuas)obtenemos un gráfico como el que aparece en la ilustración. Este tipo de diagramas reciben el nombre de diagramas de estado. En él se observa un punto llamado punto triple en el que existen a la vez los estados sólido, líquido, y gaseoso. Para una presión determinada(por ejemplo la presión atmosférica )normal su presión de vapor es igual a la presión atmosférica en el que se ve en los cambios de estado. Algunas substancias presenta el paso directo de sólio a gas , si la presión atmosférica es menor a la de su punto triple.
Contenido
Grafo dirigido
Una forma clásica de un diagrama de estados para una máquina de estados finitos es un grafo dirigido con los siguientes elementos:
Estados Q: un conjunto finito de vertices representados normalmente por círculos y etiquetados con símbolos designadores únicos o palabras escritas dentro de ellos (Booth (1967) p. 69, Hopcroft y Ullman (1979) p. 16, Sipser (2006) p. 34).
Símbolos de Entrada Σ: una colección finita de "símbolos" de entrada o designadores Σ (Booth, Hopcroft y Ullman, Sipser). Para una Autómata finito (AFD), Máquina de Estados Finitos no Determinista (AFN), Máquina de Estados Finita no Determinista Generalizada (GNFA), o una Máquina de Moore, la entrada está significada en cada arista, normalmente cerca del estado originador. Para una Máquina de Mealy, la entrada y la salida están significados sobre cada arista normalmente separados con una barra "/":
- las etiquetas de entrada y salida Mealy sobre cada arista (flecha): "1/0" designa que el símbolo "1" causó el símbolo "0" como salida.
Símbolos de Salida Z: una colección finita de "símbolos" de salida o designadores (Booth, Hopcroft y Ullman, Sipser). Para una Máquina de Mealy, la entrada y la salida están significados en cada arista como puede verse a continuación. Para una Máquina de Moore la salida del estado está escrita normalmente dentro del círculo del estado, separado del designador del estado con una barra "/".
- Ejemplo: Si un estado tiene varias salidas el diagrama debe reflejar esto : e.g. "q5/1,0" designa que el estado q5 tiene salidas a=1, b=0. Este designador será escrito dentro del círculo del estado.
La "Función de Salida ω" representa el mapeado ω de símbolos de entrada I x estados Q en símbolos de salida Z (Booth).
Aristas δ: representa las "transiciones" entre dos estados causados por la entrada (identificados sus símbolos dibujados en los "aristas"). Un 'arista' está dibujado normalmente como una flecha dirigda desde el estado presente hacia el siguiente estado. δ representa el mapeado de los símbolos de entrada I x estados Q en los símbolos de salida Z (Booth, Hopcroft y Ullman, Sipser).
Estado inicial qo: (no visto en los ejemplos anteriores). El estado inicial qo está representado normalmente por una "flecha apuntándolo desde ninguna parte" (cf Sipser (2006) p. 34, Hopcroft y Ullman (1979) p. 16). En textos antiguos (e.g. Booth (1969), McCluskey (1965), Hill y Peterson (1974)) el estado inicial no se mostraba y era inferido del texto.
Estado(s) de Aceptación F: Si se usa -- una colección de círculos dobles usados para designar los estados de aceptación(Hopcroft y Ullman, Sipser). A veces la función de el/los estado/s de aceptación se entiende como estado/s"Final/es" (cf Hopcroft y Ullman (1979) Figure 2.15, p. 33).
Ejemplos
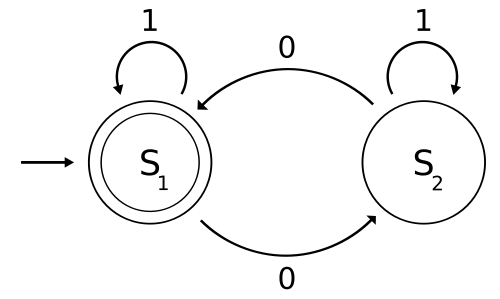
Máquinas DFA, NFA, GNFA, o Moore
S1 y S2 son estados y S1 es un estado de aceptación. Cada arista está etiquetado con la entrada.
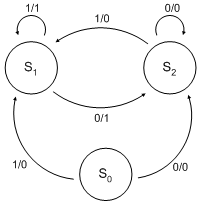
Máquina de Mealy
S0, S1, y S2 son estados. Cada flecha está etiquetado con "j / k" donde j es la entrada y k es la salida.
Cuadro de estados Harel
Los cuadros de estados(statecharts) Harel (desarrollados en 1987 por David Harel) están ganando en uso amplio dado que una variante ha llegado a ser parte del UML. El tipo de diagrama permite modelar superestados, diagramas de estados concurrentes y e.g. modelar las actividades como parte de un estado.
Los diagramas de estados clásicos son llamados diagramas "or", debido a que la máquina sólo puede estar en un estado o en otro. Con los cuadros de estados Harel es posible modelar máquinas "and", donde una máquina está en dos o más estados al mismo tiempo. Esto es debido a la posibilidad de tener superestados.
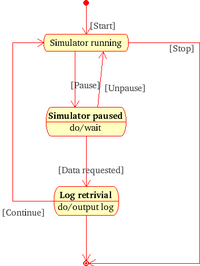
Diagrama de estados UML
Lenguaje Unificado de Modelado (UML) especifica una notación estandarizada para diagramas de estado que puede utilizarse para describir clases, sistemas, subsistemas o incluso procesos de negocio. Los elementos básicos de notación que pueden usarse para componer un diagrama son:
- Círculo lleno, apuntando a un estado inicial
- Círculo hueco que contiene un círculo lleno más pequeño en el interior, indicando el estado final (si existiera)
- Rectángulo redondeado, denotando un estado. En la parte superior del rectángulo está el nombre del estado. Puede contener una línea horizontal en la mitad, debajo de la cual se indican las actividades que se hacen en el estado
- Flecha, denotando transición. El nombre del evento (si existiera) que causa esta transición etiqueta el cuerpo de la flecha. Se puede añadir una expresión de Guarda, encerrada en corchetes( [] ) denotando que esta expresión debe ser cierta para que la transición tenga lugar. Si se realiza una acción durante la transición, se añade a la etiqueta después de "/". NombreDeEvento[ExpresiónGuarda]/acción
- Línea horizontal gruesa con x>1 líneas entrando y 1 línea saliendo o 1 línea entrando y x>1 líneas saliendo. Estas denotan Unión/Separación, respectivamente.
Referencias
- David Harel's home page
- D. Harel. Statecharts: A visual formalism for complex systems. Science of Computer Programming, 8(3):231--274, June 1987.
- Introduction to UML 2 State Machine Diagrams by Scott W. Ambler
- UML 2 State Machine Diagram Guidelines by Scott W. Ambler
- Michael Sipser (2006), Introduction to the Theory of Computation, Second Edition, Thomson Course Technology, Boston. ISBN-13: 978-0-534-95097-2, ISBN-10: 0-534-95097-3.
- John Hopcroft and Jeffrey Ullman (1979) Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing Company, Reading Mass, ISBN 0-201-02988-X.
- Taylor Booth (1967) Sequential Machines and Automata Theory, John Wiley and Sons, New York. Library of Congress Catalog Card Number: 67-25924.
Categorías: UML | Teoría de grafos
Wikimedia foundation. 2010.