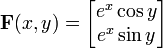Difeomorfismo local

Difeomorfismo local

Difeomorfismo local

En matemáticas, un difeomorfismo local es una aplicación diferenciable f : M → N entre variedades diferenciables tal que, para cada punto p de M, existe un entorno abierto U de p tal que f(U) es abierto en N y f|U : U → f(U) (restricción de f a U) es un difeomorfismo.

Destaquemos que:

  • todo difeomorfismo local es también un homeomorfismo local, luego será una aplicación abierta.
  • Un difeomorfismo local y biyectivo será un difeomorfismo.

De acuerdo con el teorema de la función inversa, una aplicación diferenciable f : M → N es un difeomorfismo local si y sólo si la aplicación tangente Tpf : TpM → Tf(p)N es un isomorfismo lineal para todo punto p de M. En particular, esto implica que M y N deben tener la misma dimensión.

No todo difeomorfismo local es un difeomorfismo (global). Baste como ejemplo la aplicación F de R2 en R2 definida por

\mathbf{F}(x,y) = \begin{bmatrix} {e^x \cos y}\\ {e^x \sin y}\\ \end{bmatrix}

cuyo determinante jacobiano es no nulo en todo punto. Mediante el teorema de la función inversa podemos comprobar que es un difeomorfismo local. Pero no es inyectiva, puesto que f(x,y)=f(x,y+2kπ), por lo tanto no es un difeomorfismo.

Obtenido de "Difeomorfismo local"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Homeomorfismo local — En topología, un homeomorfismo local es una aplicación de un espacio topológico en otro que respeta localmente la estructura topológica de los dos espacios. De un modo más preciso, diremos que una aplicación continua f : X → Y es un… …   Wikipedia Español

  • Variedad diferenciable — En Geometría y Topología, una variedad diferenciable es un tipo especial de variedad topológica, a la que podemos extender las nociones de cálculo diferencial que normalmente usamos en . En una variedad diferenciable M podremos definir lo que es… …   Wikipedia Español

  • Teorema de la función inversa — En la rama de la matemática denominada análisis matemático, el teorema de la función inversa proporciona las condiciones suficientes para que una aplicación sea invertible localmente en un entorno de un punto p en términos de su derivada en dicho …   Wikipedia Español

  • Homeomorfismo — Ejemplo clásico de dos figuras homeomorfas: Una taza de café con un asa y un dónut o toro. No debe confundirse con homomorfismo. En topología, un homeomorfismo (del griego ὅμοιος (homoios) = misma y μορφή (morphē) = forma) es una biyeccion entre… …   Wikipedia Español

  • Sistema de coordenadas — Un sistema de coordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un espacio euclídeo o más generalmente variedad diferenciable. En física se usan normalmente sistemas de coordenadas… …   Wikipedia Español

  • Atlas (matemáticas) — Un atlas es un conjunto de cartas (entornos de coordenadas) que proveen de estructura localmente euclídea a un espacio topológico, una carta local que contiene a un punto P define un conjunto de coordenadas curvilíneas en el entorno de P. Cada… …   Wikipedia Español

  • Topología simpléctica — La topología simpléctica es aquella parte de la matemática referida al estudio de las variedades simplécticas. Estas variedades se presentan naturalmente en la formulación hamiltoniana de la mecánica clásica, que proporciona una de las… …   Wikipedia Español

  • Grupo de Lie — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”