Efecto Compton

Efecto Compton

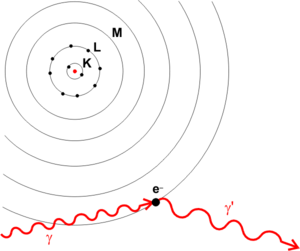
El efecto Compton consiste en el aumento de la longitud de onda de un fotón de rayos X cuando choca con un electrón libre y pierde parte de su energía. La frecuencia o la longitud de onda de la radiación dispersada depende únicamente de la dirección de dispersión.

Compton-effekt1.png

Contenido

Descubrimiento y relevancia histórica

El Efecto Compton fue estudiado por el físico Arthur Compton en 1923, quién pudo explicarlo utilizando la noción cuántica de la radiación electromagnética como cuantos de energía y la mecánica relativista de Einstein. El efecto Compton constituyó la demostración final de la naturaleza cuántica de la luz tras los estudios de Planck sobre el cuerpo negro y la explicación de Albert Einstein del efecto fotoeléctrico. Como consecuencia de estos estudios Compton ganó el Premio Nobel de Física en 1927.

Este efecto es de especial relevancia científica, ya que no puede ser explicado a través de la naturaleza ondulatoria de la luz. La luz debe comportarse como partícula para poder explicar estas observaciones, por lo que adquiere una dualidad onda corpúsculo característica de la mecánica cuántica.

Formulación matemática

La variación de longitud de onda de los fotones dispersados, Δλ, puede calcularse a través de la relación de Compton:

\Delta \lambda = \frac{h}{m_e c} \left(1-\cos \theta \right),

donde h es la constante de Planck, me es la masa del electrón, c es la velocidad de la luz y θ es el ángulo entre los fotones incidentes y dispersados.

Esta expresión proviene del análisis de la interacción como si fuera una colisión elástica y su deducción requiere únicamente la utilización de los principios de conservación de energía y momento. La cantidad h / mec = 0.0243 Å, se denomina longitud de onda de Compton. Para los fotones dispersados a 90º, la longitud de onda de los rayos X dispersados es justamente 0.0243 Å mayor que la línea de emisión primaria.

Deducción matemática

La deducción de la expresión para Δλ (llamada a veces corrimiento de Compton) puede hacerse considerando la naturaleza corpuscular de la radiación y las relaciones de la mecánica relativista. Consideremos un fotón de longitud de onda λ y momentum h / λ dirigiéndose hacia un electrón en reposo (masa en reposo del electrón me). La Teoría de la Relatividad Especial impone la conservación del cuadrimomentum p^\mu=(E/c, \vec p). Si λ' es la longitud de onda del fotón dispersado y \vec p es el momentum del electrón dispersado se obtiene:

\frac{h}{\lambda'}sen\theta=p\,sen\phi
\frac{h}{\lambda}=p\,cos\phi+\frac{h}{\lambda'}\,cos\theta

Donde θ y ϕ son, respectivamente, los ángulos de dispersión del fotón y del electrón (medidos respecto de la dirección del fotón incidente). La primera de las ecuaciones anteriores asegura la conservación de la componente del momentum perpendicular a la dirección incidente, la segunda hace lo mismo para la dirección paralela. La conservación de la energía da:

\frac{hc}{\lambda}+m_e\,c^2=\frac{hc}{\lambda'}+\sqrt{m_e^2\,c^4+c^2\,p^2}

Lo que sigue es un trabajo de Álgebra elemental. De las ecuaciones de conservación del momentum es fácil eliminar φ para obtener:

p^2=h^2(\frac{1}{\lambda^2}+\frac{1}{\lambda'^2}-\frac{2}{\lambda\,\lambda'}cos\theta )

En la expresión para la conservación de la energía hacemos:

[hc(\frac{1}{\lambda}-\frac{1}{\lambda'})+m_e\,c^2]^2=m_e^2c^4+c^2p^2

Reemplazando la expresión para p2 hallada anteriormente y luego de algunas operaciones se llega a la expresión para el corrimiento de Compton con \displaystyle{\Delta \lambda=\lambda'-\lambda}

Efecto Compton inverso

También puede ocurrir un Efecto Compton inverso; es decir, que los fotones disminuyan su longitud de onda al chocar con electrones. Pero para que esto suceda es necesario que los electrones viajen a velocidades cercanas a la velocidad de la luz y que los fotones tengan altas energías.

La principal diferencia entre los dos fenómenos es que durante el Efecto Compton "convencional", los fotones entregan energía a los electrones, y durante el inverso sucede lo contrario.

Este efecto puede ser una de las explicaciones de la emisión de rayos X en supernovas, quasars y otros objetos astrofísicos de alta energía.

Enlaces externos

Animations and Simulations


Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • efecto Compton — proceso principal de interacción de los fotones con el tejido en el rango de la radiación diagnóstica y terapéutica Diccionario ilustrado de Términos Médicos.. Alvaro Galiano. 2010 …   Diccionario médico

  • Efecto Compton — El efecto Compton consiste en el aumento de la longitud de onda de un fotón de rayos X cuando choca con un electrón libre y pierde parte de su energía. La frecuencia o la longitud de onda de la radiación dispersada depende únicamente de la… …   Enciclopedia Universal

  • Compton — Compton, Arthur Holly Compton, efecto * * * (as used in expressions) Compton, Arthur (Holly) Compton, efecto Compton Burnett, Dame Ivy Crick, Francis (Harry Compton) Mackenzie, Sir (Edward Montague) Compton …   Enciclopedia Universal

  • Efecto — Saltar a navegación, búsqueda Para la técnica deportiva, véase chanfle, massé y efecto Magnus. La palabra efecto (del latín effectus) tiene una gran cantidad de significados, ligados muchos de ellos a la experimentación científica, porque su… …   Wikipedia Español

  • Compton, Arthur Holly — ► (1892 1962) Físico estadounidense. Fue premio Nobel de Física en 1927, compartido con Ch. T. R. Wilson por el descubrimiento del efecto Compton …   Enciclopedia Universal

  • Compton, Arthur (Holly) — (10 sep. 1892, Wooster, Ohio, EE.UU.–15 mar. 1962, Berkeley, Cal.). Físico estadounidense. Enseñó en la Universidad de Chicago (1923.–45) y más tarde se desempeñó como rector (1945.–54) y profesor (1953.–61) en la Washington University. Es… …   Enciclopedia Universal

  • Efecto fotoeléctrico — Saltar a navegación, búsqueda Diagrama del efecto fotoeléctrico. Los fotones incidentes son absorbidos por los electrones del medio dotándoles de energía suficiente para escapar de éste. El efecto fotoeléctrico consiste en la emisión de… …   Wikipedia Español

  • efecto — (Del lat. effectus < efficere, producir un efecto < facere, hacer.) ► sustantivo masculino 1 Resultado de una causa: ■ tomar el sol en exceso puede causar efectos nocivos para la piel. SINÓNIMO consecuencia resultado secuela ANTÓNIMO causa… …   Enciclopedia Universal

  • Compton, efecto — ► FÍSICA NUCLEAR Proceso, descubierto por A. H. Compton, de interacción entre radiación y materia, consistente en el choque entre un fotón y un electrón. Parte de la energía del fotón incidente es cedida al electrón de manera que, después del… …   Enciclopedia Universal

  • efecto de Compton — Cuando los rayos X chocan con la superficie de un material de peso atómico bajo, parte de los rayos X dispersas son de un largo de onda mayor que los rayos originales. Compton, que fue el primero en observar este fenómeno, explicó que cuando un… …   Diccionario ecologico

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”