Ley de Planck

Ley de Planck
Ley de Planck para cuerpos a diferentes temperaturas.
Curvas de emisión de cuerpos negros a diferentes temperaturas comparadas con las predicciones de la física clásica anteriores a la ley de Planck.

La intensidad de la radiación emitida por un cuerpo negro con una temperatura T viene dada por la ley de Planck:

I(\nu ,T) = \frac{2h\nu^{3}}{c^2}\frac{1}{e^{\frac{h\nu}{kT}}-1}

donde I(\nu)\delta\nu \, es la cantidad de energía por unidad de área, unidad de tiempo y unidad de ángulo sólido emitida en el rango de frecuencias entre \nu \, y \nu + \delta \nu \, .

El siguiente cuadro muestra la definición de cada símbolo en unidades de medidas del SI y CGS:

Símbolo Significado Unidades SI Unidades CGS
I, I' \, Radiancia espectral, o es la cantidad de energía por unidad de superficie, unidad de tiempo y unidad de ángulo sólido por unidad de frecuencia o longitud de onda (tal como se especifique) J m-2 sr-1 erg cm-2 sr-1
\nu \, frecuencia hercios (Hz) hercios
\lambda \, longitud de onda metro (m) centímetros (cm)
T \, temperatura del cuerpo negro Kelvin (K) kelvin
h \, Constante de Planck julio x segundo (J s) ergio x segundo (erg s)
c \, velocidad de la luz metros / segundo (m / s) centímetros / segundo (cm / s)
e \, base del logaritmo natural, 2,718281 ... adimensional adimensional
k \, Constante de Boltzmann julios por kelvin (J / K) ergios por kelvin (erg / K)

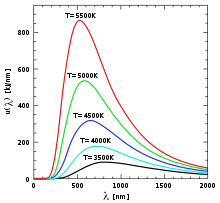
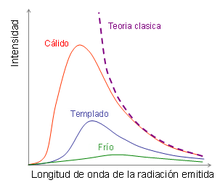
La longitud de onda en la que se produce el máximo de emisión viene dada por la ley de Wien y la potencia total emitida por unidad de área viene dada por la ley de Stefan-Boltzmann. Por lo tanto, a medida que la temperatura aumenta el brillo de un cuerpo cambia del rojo al amarillo y al azul.

Contenido

Poder emisivo

Se llama Poder emisivo espectral de un cuerpo E(\nu, T) \, a la cantidad de energía radiante emitida por la unidad de superficie y tiempo entre las frecuencias \nu \, y \nu + \delta \nu \, . Se trata por tanto de una potencia.

E(\nu ,T)= \pi \cdot I(\nu , T)=\frac{2\pi h\nu^{3}}{c^3}\frac{1}{e^{\frac{h\nu}{kT}}-1}

Consideremos el intervalo de frecuencias entre \nu \, y \nu + \delta \nu \, y sea dE el poder emisivo del cuerpo en el intervalo de frecuencias.

dE=E(\nu ,T) d \nu \,

considerando que la longitud de onda se relaciona con la frecuencia:

\lambda=\frac{c}{\nu} y por tanto \quad d\nu=\frac{-c}{(\lambda)^2}d\lambda

resulta que el poder emisivo espectral en función de la longitud de onda es:

E(\lambda,T)={C_1 \over \lambda^5 \cdot (e^{C_2 \over \lambda \cdot T}-1)}

donde las constantes valen en el Sistema Internacional de Unidades o sistema MKS:

C_1=2 \pi h c^2=3,742 \cdot 10^{-16}\; {\rm W \cdot m^2}
C_2={h c \over k}=1,4385 \cdot 10^{-2}\; {\rm m \cdot K}

De la Ley de Planck se derivan la ley de Stefan-Boltzmann y la ley de Wien.

Unidades

Si usamos el Sistema Internacional de Unidades o sistema MKS, la longitud de onda se expresaría en metros, el poder emisivo en un intervalo de frecuencias dE en \frac{W}{m^2} y el poder emisivo por unidad de longitud o poder emisivo espectral E(\lambda ,T)=\frac{dE}{d\lambda} en \frac{W}{m^3} vatios por metro cúbico.


No es común expresar la longitud de onda en metros. Con frecuencia resulta cómodo expresarla en nanómetros llamados antiguamente milimicras 1nm = 10 − 9m, pero manteniendo la unidad de dE en \frac{W}{m^2}, en este caso:

\frac {C_1 \cdot d\lambda }{\lambda ^5}=3,742 \cdot 10^{20} {W \cdot m^2} \cdot \frac {d\lambda (nm)}{\lambda ^5 (nm)}\,
\frac {C_2}{\lambda }=1,439 \cdot 10^7 \frac {m \cdot K}{\lambda (nm)}


Si queremos expresar el poder emisivo espectral E(\lambda ,T) \, en la unidad práctica \frac{cal}{cm^2 \cdot mto \cdot \mu m}, donde 1μm = 10 − 6m es 1 micrómetro o micra se puede usar el factor de conversión:

1 \frac{W}{m^3}=1,434 \cdot 10^{-9}\frac{cal}{cm^2 \cdot mto \cdot \mu m}

Ejemplos de la ley de Planck

  • La aplicación de la Ley de Planck al Sol con una temperatura superficial de unos 6000 K nos lleva a que el 99% de la radiación emitida está entre las longitudes de onda 0,15 μm (micrómetros o micras) y 4 micras y su máximo (Ley de Wien) ocurre a 0,475 micras. Como 1 nanómetro 1 nm = 10-9 m=10-3 micras resulta que el Sol emite en un rango de 150 nm hasta 4000 nm y el máximo ocurre a 475 nm. La luz visible se extiende desde 380 nm a 740 nm. La radiación ultravioleta u ondas cortas iría desde los 150 nm a los 380 nm y la radiación infrarroja u ondas largas desde las 0,74 micras a 4 micras.
  • La aplicación de la Ley de Planck a la Tierra con una temperatura superficial de unos 288 K (15 °C) nos lleva a que el 99% de la radiación emitida está entre las longitudes de onda 3 μm (micrómetros o micras) y 80 micras y su máximo ocurre a 10 micras. La estratosfera de la Tierra con una temperatura entre 210 y 220 K radia entre 4 y 120 micras con un máximo a las 14,5 micras.

Véase también

Enlaces externos

Bibliografía

  • Emilio A. Caimi "La energía radiante en la atmósfera" EUDEBA 1979

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать курсовую

Mira otros diccionarios:

  • Ley de Planck — La intensidad de la radiación emitida por un cuerpo negro con una temperatura T viene dada por la ley de Planck: donde ● es la cantidad de energía por unidad de área, unidad de tiempo y unidad de ángulo sólido emitida en el rango de frecuencias… …   Enciclopedia Universal

  • Ley de desplazamiento de Wien — Ley de Wien. La ley de desplazamiento de Wien es una ley de la física. Especifica que hay una relación inversa entre la longitud de onda en la que se produce el pico de emisión de un cuerpo negro y su temperatura. d …   Wikipedia Español

  • Ley de Rayleigh-Jeans — Comparación de la Ley de Rayleigh Jeans con la Ley de Wien y la Ley de Planck, por un cuerpo de temperatura de 8 mK. En física, la Ley de Rayleigh Jeans, primeramente propuesta por los comienzos del siglo XX, los intentos de describir la… …   Wikipedia Español

  • Ley de Stefan-Boltzmann — La ley de Stefan Boltzmann establece que un cuerpo negro emite radiación térmica con una potencia emisiva superficial (W/m²) proporcional a la cuarta potencia de su temperatura: Donde Te es la temperatura efectiva o sea la temperatura absoluta de …   Wikipedia Español

  • Planck — Planck, Max Planck, constante de Planck, ley de la radiación de …   Enciclopedia Universal

  • Ley científica — Una ley científica es una proposición científica que afirma una relación constante entre dos o más variables o factores, cada uno de las cuales representa (al menos parcial e indirectamente) una propiedad de sistemas concretos. Se define también… …   Wikipedia Español

  • Planck, Max (Karl Ernst Ludwig) — (23 abr. 1858, Kiel, Schleswig, Alemania–4 oct. 1947, Gotinga, Alemania Occidental). Físico alemán. Estudió en las universidades de Munich y Kiel, llegando luego a ser profesor de física teórica en la Universidad de Berlín (1889–1928). Su trabajo …   Enciclopedia Universal

  • Max Planck — Para el satélite artificial de la Agencia Espacial Europea, véase Planck Surveyor. Max Karl Ernest Ludwig Planck …   Wikipedia Español

  • Constante de Planck — Valores de h Unidades 6.62606896(33) ×10 34 J·s 4.13566733(10)×10 15 eV·s 6.62606896(33) ×10 27 ergio·s Valores de ħ Unidades 1.054571628(53) ×10 34 J·s …   Wikipedia Español

  • Planck, ley de la radiación de — ► FÍSICA NUCLEAR Relación matemática que expresa la distribución de energía radiante que emite un cuerpo caliente …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”