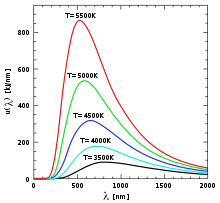
Ley de desplazamiento de Wien

Ley de desplazamiento de Wien
Ley de Wien.

La ley de desplazamiento de Wien es una ley de la física. Especifica que hay una relación inversa entre la longitud de onda en la que se produce el pico de emisión de un cuerpo negro y su temperatura.

\lambda_\mbox{max} = \frac{0,0028976\ \mbox{m} \cdot \mbox{K}}{T}

donde T es la temperatura del cuerpo negro en Kelvin (K) y λmax es la longitud de onda del pico de emisión en metros.

Las consecuencias de la ley de Wien es que cuanta mayor sea la temperatura de un cuerpo negro menor es la longitud de onda en la cual emite. Por ejemplo, la temperatura de la fotosfera solar es de 5780 K y el pico de emisión se produce a 475 nm = 4,75 · 10-7 m. Como 1 angstrom 1 Å= 10-10 m = 10-4 micras resulta que el máximo ocurre a 4750 Å. Como el rango visible se extiende desde 4000 Å hasta 7400 Å, esta longitud de onda cae dentro del espectro visible siendo un tono de verde. Sin embargo, debido a la Dispersión de Rayleigh de la luz azul por la atmósfera, la componente azul se separa distribuyéndose por la bóveda celeste y el Sol aparece amarillento.

Deducción de la Ley de Wien

La constante c de Wien esta dada en Kelvin x metro.

Esta ley fue formulada empíricamente por Wilhelm Wien. Sin embargo, hoy se deduce de la ley de Planck para la radiación de un cuerpo negro de la siguiente manera:

E(\lambda,T)={C_1 \over \lambda^5 \cdot (e^{C_2 \over \lambda \cdot T}-1)}={C_1 \cdot \lambda^{-5}\over (e^{C_2 \over \lambda \cdot T}-1)}

donde las constantes valen en el Sistema Internacional de Unidades o sistema MKS:

C_1=2 \pi h c^2=3,742 \cdot 10^{-16}\; {\rm W \cdot m^2}
C_2={h c \over k}=1,4385 \cdot 10^{-2} \ \mbox{m} \cdot \mbox{K} = 1,4385 \cdot 10^4 \ \mu \mbox{m} \cdot \mbox{K}

Para hallar el máximo la derivada de la función con respecto a λ tiene que ser cero.

{\partial (E(\lambda,T)) \over \partial \lambda}=0

Basta con utilizar la regla de derivación del cociente y como se tiene que igualar a cero, el numerador de la derivada será nulo es decir:

\frac {c_2}{\lambda \cdot T}=5 \cdot (1-e^{-C_2 \over \lambda \cdot T})

Si definimos

x\equiv{c_2\over\lambda T }

entonces

{x\over 1-e^{-x}}-5=0

Esta ecuación no se puede resolver mediante funciones elementales. Como una solución exacta no es importante podemos optar por soluciones aproximadas. Se puede hallar fácilmente un valor aproximado para x:

Si x es grande resulta que aproximadamente e^{-x}=0 \, así que x esta cerca de 5. Así que aproximadamente x=5(1-e^{-5})=4,9663 \,.

Utilizando el método de Newton o de la tangente:

x = 4,965114231744276\ldots

De la definición de x resulta que:

\lambda_{\max} \cdot T=\frac{c_2}{x}=\frac{1,4385 \cdot 10^4}{4,965114231744276}=2897,6 \mu m K

Así que la constante de Wien es 2897,6 \mu m \cdot K por lo que:

\lambda_{\max} \cdot T = 2897,6 \mu m \cdot K

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Wien (desambiguación) — Saltar a navegación, búsqueda Wien es el nombre alemán para Viena, ciudad de Austria. Puede referirse a: Wilhelm Wien (1864–1928), físico alemán ganador del premio Nobel en 1911 Ley de desplazamiento de Wien, ley de la física. Aproximación de… …   Wikipedia Español

  • Wien — es el nombre alemán para Viena, ciudad de Austria. También puede referirse a: Wilhelm Wien (1864–1928), físico alemán ganador del premio Nobel en 1911. Ley de desplazamiento de Wien, ley de la física. Aproximación de Wien: proposición de la… …   Wikipedia Español

  • Constante física — En ciencias se entiende por constante física el valor de una magnitud física cuyo valor, fijado un sistema de unidades, permanece invariable en los procesos físicos a lo largo del tiempo. En contraste, una constante matemática representa un valor …   Wikipedia Español

  • Termofotovoltaico — La conversión de energía Termofotovoltaica (TPV en inglés) es un proceso de conversión directa de calor diferencial a electricidad por medio de fotones. Un sistema termofotovoltaico básico consiste en un emisor térmico y un diodo de energía… …   Wikipedia Español

  • Historia del electromagnetismo — La Historia del electromagnetismo, que es el conocimiento y el uso registrado de las fuerzas electromagnéticas, data de hace más de dos mil años. En la antigüedad ya estaban familiarizados con los efectos de la electricidad atmosférica, en… …   Wikipedia Español

  • Temperatura absoluta — La Teoría cinética de los gases establece que la energía total media de la translación de una molécula es directamente proporcional a la temperatura absoluta del gas. La Temperatura absoluta es el valor de la temperatura medida con respecto a una …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”