Dominio euclídeo

Dominio euclídeo

Dominio euclídeo

Un dominio euclídeo (o anillo euclídeo) es un par (R,φ) donde R es un dominio de integridad y φ es una aplicación norma euclídea, es decir, una aplicación 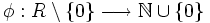\phi: R \setminus \{0\} \longrightarrow \mathbb{N} \cup \{0\} que cumple las siguientes dos condiciones:

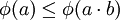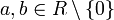  • \phi(a) \leq \phi(a \cdot b) cualesquiera que sean a,b \in R \setminus \{0\}.
  • Para cualesquiera 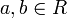a,b \in R tales que 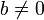b \neq 0 se cumple que existen 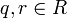q,r \in R de manera que a = bq + r si 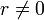r \neq 0 ha de ser φ(r) < φ(b).

Es importante señalar que la definición es exactamente esa, aun cuando en algún caso particular pueda extenderse φ a todo el conjunto R.

Ejemplos

  • Si tomamos el conjunto de los números enteros 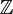\mathbb{Z} y como norma euclídea tomamos la aplicación valor absoluto | \cdot |, tenemos un dominio euclídeo.
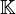  • Considerando el anillo de polinomios en una variable \mathbb{K}[x] con coeficientes en el cuerpo \mathbb{K} y como aplicación norma euclídea tomo el grado deg de cada polinomio, el resultado es un dominio euclídeo.

Véase también algoritmo de la división

Obtenido de "Dominio eucl%C3%ADdeo"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Dominio euclídeo — Un dominio euclídeo (o anillo euclídeo) es un par donde es un dominio de integridad y es una aplicación norma euclídea, es decir, una aplicación que cumple las siguientes dos condiciones: ● cualesquiera que sean . ● Para cualesquiera tales que se …   Enciclopedia Universal

  • Dominio de integridad — Saltar a navegación, búsqueda Un dominio de integridad, dominio íntegro, anillo íntegro, o sencillamente dominio (este último término es un abuso de lenguaje y puede dar lugar a confusión, ya que la palabra dominio tiene varios usos en… …   Wikipedia Español

  • Espacio euclídeo — Saltar a navegación, búsqueda El espacio euclídeo o euclidiano es el espacio matemático n dimensional usual, una generalización de los espacios de 2 (plano euclídeo) y 3 dimensiones estudiados por Euclides. Estructuralmente un espacio euclídeo es …   Wikipedia Español

  • Algoritmo de Euclides — El algoritmo de Euclides es un método antiguo y eficaz para calcular el máximo común divisor (MCD). Fue originalmente descrito por Euclides en su obra Elementos. El algoritmo de Euclides extendido es una ligera modificación que permite además… …   Wikipedia Español

  • Algoritmo de la división — Se ha sugerido que Algoritmo de la división sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. En matemáticas, y más precisamente en la aritmética, la… …   Wikipedia Español

  • Norma euclídea — Se ha sugerido que este artículo o sección sea fusionado en Dominio euclídeo (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. En un dominio íntegro D, una norma euclídea es una aplicación …   Wikipedia Español

  • Anillo de polinomios — Saltar a navegación, búsqueda Sea A un anillo y S cualquier conjunto. El conjunto A[S] de todos los objetos (1) , en donde …   Wikipedia Español

  • Entero cuadrático — En teoría de números, los enteros cuadráticos son una generalización de los enteros racionales a los cuerpos cuadráticos. Entre los ejemplos importantes se incluyen los enteros gaussianos y los enteros de Eisenstein. A pasar de que han sido… …   Wikipedia Español

  • Sistema de coordenadas — Un sistema de coordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un espacio euclídeo o más generalmente variedad diferenciable. En física se usan normalmente sistemas de coordenadas… …   Wikipedia Español

  • Variedad (matemática) — En una esfera, la suma de los ángulos de un triángulo no es igual a 180°, pues una esfera no es un espacio euclídeo. Sin embargo, localmente, las leyes de la geometría euclídea son buenas aproximaciones. Este ejemplo ilustra cómo la esfera puede… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”