Un dominio de integridad, dominio íntegro, anillo íntegro, o sencillamente dominio (este último término es un abuso de lenguaje y puede dar lugar a confusión, ya que la palabra dominio tiene varios usos en Matemática) es un anillo 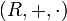que carece de elementos divisores de cero por la izquierda y de elementos divisores de cero por la derecha (con lo cual carece de elementos divisores de cero).

Un subanillo de un dominio de integridad es también un dominio de integridad.

En la literatura "antigua" se exige (a veces se sobreentiende) que el anillo es conmutativo y unitario, porque se ignoraba la existencia de anillos no conmutativos que no tuvieran divisores de cero (por la izquierda o por la derecha). Los dominios de Mal'cev son un tipo de anillos no conmutativos que carecen de elementos divisores de cero (ni por la izquierda ni por la derecha). Respecto a dominios íntegros no unitarios, el conjunto 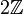es un subanillo no unitario del dominio de integridad 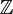. En este artículo, un dominio íntegro será siempre un anillo conmutativo y unitario (ya que así se entiende en la mayor parte de la literatura, señalándose los casos en que no se adopta estos criterios).

Todo cuerpo es dominio de integridad conmutativo y unitario. Más en general, todo anillo de división es dominio de integridad unitario.

Contenido 1 Cuerpo de cocientes de un dominio íntegro 1.1 Operaciones suma y producto en el cuerpo de cocientes 1.1.1 Suma 1.1.2 Producto 1.1.3 Distributividad 2 Divisibilidad en un dominio íntegro (conmutativo y unitario) cualquiera 2.1 Máximo común divisor y mínimo común múltiplo 2.1.1 Propiedades

Cuerpo de cocientes de un dominio íntegro

Una de las propiedades más interesantes de un dominio de integridad es la de que existe "el menor cuerpo que lo contiene". De forma más precisa:

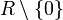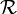Sea R un dominio íntegro (conmutativo y unitario). Denotamos por R ^* al conjunto . Establecemos en el conjunto la relación definida por 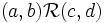cuando y sólo cuando 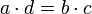. Es sencillo comprobar que 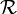es una relación de equivalencia. Denotaremos por Q(R) al conjunto cociente 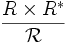, y por 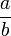a la clase de equivalencia del elemento (a,b).

Operaciones suma y producto en el cuerpo de cocientes

Suma

Definimos la aplicación 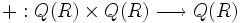de la siguiente manera: 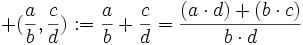, cualesquiera que sean 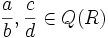. Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro y que todo elemento 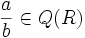tiene por elemento simétrico (elemento opuesto) a 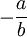. Así, (Q(R), + ) es un grupo abeliano.

Producto

Definimos la aplicación 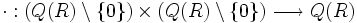de la siguiente manera: 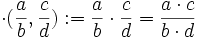, cualesquiera que sean 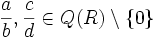. Es sencillo comprobar que es operación interna, asociativa, conmutativa, que tiene elemento neutro y que todo elemento 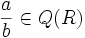tiene por elemento simétrico (elemento inverso) a . Así, 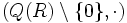es un grupo abeliano.

Distributividad

Se demuestra sin dificultad que es distributiva respecto de +. Esto hace que 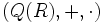quede dotado de estructura de cuerpo.

Divisibilidad en un dominio íntegro (conmutativo y unitario) cualquiera

Quizás el aspecto más interesante que ofrecen los dominios íntegros es el de poder genralizar a ellos muchas de las propiedades sobre divisibilidad que conocemos en el anillo de los números enteros .

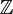En adelante, a,b,c,d,r,x,y,m,u representarán elementos en el dominio íntegro R (i.e. ).

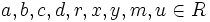Se dice que a y b son asociados si existe un 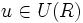de manera que 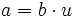. Se denota por .

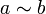Se dice que a divide a b si existe un 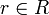de manera que 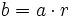. Se denota por a | b. Si a y b son asociados, entonces a divide a b y b divide a a.

Se dice que un elemento a de un dominio íntegro R es un átomo o elemento irreducible (a veces se dice simplemente que es un irreducible) de R si 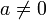, , 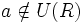y si 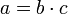entonces o bien es 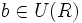o bien 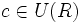(o los dos).

Se dice que un elemento a de un dominio es un elemento primo (o simplemente primo) si el ideal generado por a es ideal primo de R.

Lo cierto es que la notación es un poco confusa cuando nos referimos a los números enteros. En ese caso, el concepto de número primo corresponde con el de elemento irreducible (que además sea positivo), y tedríamos que el 0 y el 1 serían elementos primos de 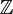, aunque no serían números primos.

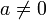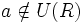Si a es elemento primo del dominio íntegro R, y entonces a es irreducible.

Máximo común divisor y mínimo común múltiplo

Sean .

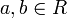• Un máximo común divisor de a y b, (denotado por mcd(a,b)) es, si existe, un elemento 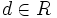de tal manera que d | a, d | b y si 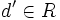es tal que d' | a y d' | b, entonces d' | d.
• Un mínimo común múltiplo de a y b, (denotado por mcm(a,b)) es, si existe, un elemento 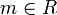de tal manera que a | m, b | m y si 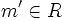es tal que a | m' y b | m', entonces m | m'.

Es de destacar que no se dice el máximo común denominador ni el mínimo común múltiplo, sino un máximo común divisor o un mínimo común múltiplo. Esto es debido a que, tal y como están definidos, un mismo par de elementos 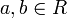pueden tener más de un máximo común divisor y más de un mínimo común múltiplo. Por otra parte, en un dominio de integridad no siempre está asegurada la existencia del mínimo común múltiplo o del máximo común denominador de dos elementos cualesquiera.

Dos elementos 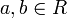se dicen coprimos si existe mcd(a,b) y además 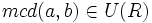(es decir, 1 es mcd(a,b)).

Propiedades

• Si d y d' son mcd(a,b), entonces 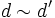. Si m y m' son mcm(a,b), entonces 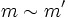. Escribiremos entonces siempre 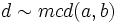en lugar de d = mcd(a,b) y 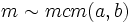en lugar de m = mcm(a,b).
• .
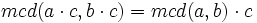• Si 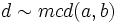entonces 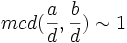(es decir, 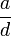y son coprimos).
• Si a y b son coprimos (i.e. 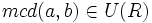), entonces, para cualquiera que sea 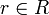se cumple que .
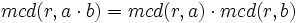• Si a | b entonces mcd(a,b) = a.
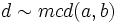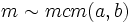• Si y entonces 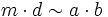(en particular esto significa que si existe máximo común divisor de dos elementos, entonces existe su mínimo común múltiplo, y viceversa).
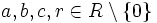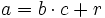• Si y , entonces .

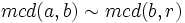Estas son las principales afirmaciones que podemos decir sobre divisibilidad en dominios de integridad sin exigir más condiciones, como que el anillo R sea dominio de factorización única, dominio de ideales principales o que sea dominio euclídeo.