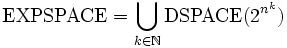- EXPSPACE
-
EXPSPACE
En teoría de la complejidad computacional, la clase de complejidad EXPSPACE es el conjunto de los problemas de decisión que pueden ser resueltos con una máquina de Turing determinista en espacio O(2p(n)), donde p(n) es una función polinomial sobre n. (Cuando se restringe p(n) como una función lineal, la clase resultante se denomina ESPACE.)
En términos de DSPACE,
La clase de complejidad EXPSPACE-completo es la clase de los problemas que están en EXPSPACE tales que todo problema de EXPSPACE tiene una transformación polinomial hacia cada uno de los problemas de EXPSPACE-completo. Dicho de otra forma, existe un algoritmo que trabaja en tiempo polinómico que transforma las instancias de un problema en las instancias del otro con la misma respuesta. El conjunto EXPSPACE-completo puede ser visto como el conjunto de los problemas más difíciles de EXPSPACE.
EXPSPACE contiene de forma estricta las clases PSPACE, NP-completo, NP y P y se cree que también contiene estrictamente el conjunto EXPTIME.
Un ejemplo de problema en EXPSPACE-completo es el de decidir si dos expresiones regulares representan lenguajes diferentes, cuando los operadores regulares utilizados son la unión, la concatenación, la clausura de Kleene (cero o más copias de una expresión), y el cuadrado (dos copias de una expresión).
Si no se incluye la clausura de Kleene, el problema es NEXPTIME-completo, que es como EXPTIME-completo, salvo que se define según las máquinas de Turing no-deterministas.
En 1980, L. Berman demostró que el problema de verificar o falsificar cualquier expresión de primer orden sobre los números reales que solo utiliza suma y comparación (pero no multiplicación) está en EXPSPACE.
Referencias
- L. Berman The complexity of logical theories, Theoretical Computer Science 11:71-78, 1980.
Categoría: Clases de complejidad
Wikimedia foundation. 2010.