- Ecuación de Pell
-
Ecuación de Pell
Una ecuación de Pell es una ecuación diofántica de la forma:
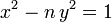
Donde n es un número entero que no es cuadrado perfecto.Estas ecuaciones fueron estudiadas ya por Arquímedes, de manera indirecta, al resolver el problema de las reses del sol. Aunque el matemático que trabajó formalmente en ellas fue Bhaskara I.
Por ejemplo, planteó el problema: "Dime, Oh matemático, cuál es el cuadrado que multiplicado por 8 se convierte - junto con la unidad - en un cuadrado?" En notación moderna, preguntó por las soluciones de la ecuación de Pell x2 - 8y2=1. Tiene la solución simple x = 3, y = 1, o acortado (x,y) = (3,1), a partir de las cuales se pueden construir más soluciones, por ejemplo, (x,y) = (17,6).
La denominación actual proviene de un error de Euler, quien atribuyó a John Pell (1610-1685) el estudio profundo de estas ecuaciones, cuando realmente fue William, Vizconde de Brouncker (c. 1620-1684) el matemático que realizó el trabajo. Aunque Brouncker utilizó fracciones continuas y obtuvo soluciones fue Lagrange el matemático que demostró que tenía infinitas soluciones y pulió el método de la fracción continua.
Auque esta ecuación se considera resuelta, no es posible decir que el problema haya sido solucionado exhaustivamente. Existen algunas dificultades. El hallazgo de soluciones se basa en el estudio de las unidades en
![\mathbb{Z}{[\sqrt{n}]}](/pictures/eswiki/100/dc67bc23c5af11187d40731928f5d0f2.png) o el desarrollo en fracción continua de n.[1] [2]
o el desarrollo en fracción continua de n.[1] [2]Referencias
Bibliografía
- Guelfond, A. O. (1979). Resolución de Ecuaciones en Números Enteros. Moscú: Editorial Mir, Colección Lecciones Populares de Matemáticas. ISBN no posee.
- Koch, Helmut (2000). Number Theory. Algebraic Numbers and Functions. AMS Bookstore - American Mathematical Society. ISBN 0-8218-2054-0, ISBN 978-0-8218-2054-4.
Enlaces externos
Categoría: Ecuaciones diofánticas
Wikimedia foundation. 2010.

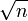 como fracción continua.
como fracción continua.