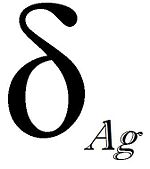Número plateado

El número plateado o razón plateada es una constante matemática. Su nombre es una alusión a la razón áurea; análoga a la forma en que el número áureo es la proporción limitante de la sucesión de Fibonacci, el número plateado es la proporción limitante de la sucesión de Pell. El término número plateado a veces es confundido con el número plástico.

Contenido

1 Definición
- 1.1 Fracción continua
2 Propiedades
- 2.1 No equidistribución mod 1
- 2.2 Potencias de la razón plateada
3 Expresiones plateadas
- 3.1 Propiedades de la razón plateada
4 Rectángulos plateados
5 Referencias

Definición

La razón plateada ( $δ S$ ) es un número irracional definido por la suma de 1 y la raíz cuadrada de 2. Esto es:

$\delta_S = 1 + \sqrt{2} \approx 2.414\, 213\, 562\, 373\, 095\, 048\, 801\, 688\, 724\, 210...$

Se sigue de esta definición que:

$(\delta_S-1)^2=2\,$

Fracción continua

En fracción continua, la razón plateada $[2,2,2,...]$ se expresa:

$\delta_S = 2 + \frac{1}{2 + \frac{1}{2 + \frac{1}{2 + \cdots}}}$

Propiedades

No equidistribución mod 1

En las aproximaciones diofánticas, la secuencia de partes fraccionales de

xⁿ, n = 1, 2, 3, ...

Se puede ver que la equidistribución mod 1, para casi todos los números reales que x > 1. La razón plateda es una excepción.

Potencias de la razón plateada

Las potencias inferiores de la razón plateada son:

$\!\ \delta_S^0 = 1$

$\delta_S^1 = \delta_S + 0$

$\delta_S^2 = 2\delta_S + 1$

$\delta_S^3 = 5\delta_S + 2$

$\delta_S^4 = 12\delta_S + 5$

Las potencias continúan con el patrón

$\!\ \delta_S^n = K_n\delta_S + K_{(n-1)}$

donde

$\!\ K_n = 2 K_{(n-1)} + K_{(n-2)}$

Por ejemplo, empleando esta propiedad:

$\!\ \delta_S^5 = 29\delta_S + 12$

Empleando $\!\ K_0 = 1$ y $\!\ K_1 = 2$ como condición inicial, una fórmula tipo-Binet daría la solución en forma recurrente...

$\!\ K_n = 2 K_{(n-1)} + K_{(n-2)}$

lo cual acaba siendo...

$\!\ K_n = \frac{1}{2\sqrt{2}} {(\delta_S^{n+1} - {(2-\delta_S)}^{n+1})}$

Expresiones plateadas

La expresión general $[n,n,n,\dots]=\frac{1}{2}\left(n+\sqrt{n^2+4}\right)$ se conoce con el nombre de expresión plateada. La razón dorada es una expresión plateada para $n = 1$ , mientras que la razón plateada es para $n = 2$ . Los valores de las diez primeras razones plateadas se muestran a la derecha.^[1]

Expresiones plateadas
0	0 + √1	1
1	½ + √1¼	1.618033989
2	1 + √2	2.414213562
3	1½ + √3¼	3.302775638
4	2 + √5	4.236067978
5	2½ + √7¼	5.192582404
6	3 + √10	6.162277660
7	3½ + √13¼	7.140054945
8	4 + √17	8.123105626
9	4½ + √21¼	9.109772229

Propiedades de la razón plateada

Estas propiedades sólo son válidas para enteros m; para números no enteros las propiedades son similares, pero difieren ligeramente. Las propiedades mostradas más abajo para las potencias de la razón plateada son una consecuencia de las propiedades que muestran. Para la expresión de la razón plateada S de m, la propiedad puede generalizarse como

$\!\ S_{m}^n = K_{n}S_{m} + K_{(n-1)}$

donde

$\!\ K_n = mK_{(n-1)} + K_{(n-2)}$

Empleando las condiciones iniciales $\!\ K_0 = 1$ and $\!\ K_1 = m$ , esta relación recurrente llega a ser ...

$\!\ K_n = \frac{1}{\sqrt{m^2 + 4}} {(S_{m}^{n+1} - {(m-S_{m})}^{n+1})}$

Las potencias de la razón plateada poseen otras propiedades interesantes:

Si n es un número entero positivo y par:

$\!\ {{S_{m}^n - \lfloor S_{m}^n \rfloor} \over S_{m}^{-n}} = S_{m}^n - 1$

Además,

$\!\ {1 \over {S_{m}^4 - \lfloor S_{m}^4 \rfloor}} + \lfloor S_{m}^4 - 1 \rfloor = S_{(m^4 + 4m^2 + 1)}$

$\!\ {1 \over {S_{m}^6 - \lfloor S_{m}^6 \rfloor }} + \lfloor S_{m}^6 - 1 \rfloor = S_{(m^6 + 6m^4 + 9m^2 +1)}$

También,

$\!\ S_{m}^3 = S_{(m^3 + 3m)}$

$\!\ S_{m}^5 = S_{(m^5 + 5m^3 + 5m)}$

$\!\ S_{m}^7 = S_{(m^7 + 7m^5 + 14m^3 + 7m)}$

$\!\ S_{m}^9 = S_{(m^9 + 9m^7 + 27m^5 + 30m^3 + 9m)}$

$\!\ S_{m}^{11} = S_{(m^{11} + 11m^9 + 44m^7 + 77m^5 + 55m^3 + 11m)}$

La media de la razón plateada S de m también tiene la propiedad que:

$\!\ 1/S_{m} = S_{m}-m$

lo cual significa que la media de la expresión plateada tiene la misma parte decimal que la correspondiente expresión plateada. Empleando esta propiedad, la expresión de la razón plateada definida para todos los números debe satisfacer:

$\!\ x \equiv x^{-1} \pmod 1$

Si expandimos la expresión de la razón dorada S de m tal que

$\!\ S_{m} = a + b$

donde a es la parte entera de S y b, entonces la siguiente propiedad es cierta:

$\!\ S_{m}^2 = a^2 + mb + 1.$

Por ser (para todos los m mayores que 0), la parte entera de S_m = m, a=m. Para m>1, donde tenemos que

$\!\ S_{m}^2 = ma + mb + 1$

$\!\ S_{m}^2 = m(a+b) + 1$

$\!\ S_{m}^2 = m(S_{m}) + 1$

Por lo tanto, la expresión de la razón plateada de m es una solución de la ecuación

$\!\ x^2 - mx - 1 = 0$

Es interesante resaltar que la expresión de la expresión S of −m es la inversa de la expresión S de m.

$\!\ {1/S_m} = S_{(-m)} = S_m - m.$

Otro resultado interesante se puede obtener mediante un ligero cambio en la fórmula de la expresión. Si consideramos un número

$\!\ \frac{1}{2}\left(n+\sqrt{n^2+4c}\right) = R$

entonces las siguientes propiedades son ciertas:

$\!\ R - \lfloor R \rfloor = c/R$ si c es real,

$\!\ \left({1 \over R}\right)c = R - \lfloor \mathrm{Re}(R) \rfloor$ si c es un múltiplo de i.

Rectángulos plateados

Un rectángulo cuya relación de aspecto entre los lados sea igual a la razón plateada se denomina rectángulo plateado, por analogía con la razón dorada. Confusamente, el “rectángulo de plata” se puede también referir a un rectángulo en la proporción 1:√2, también conocido como “un rectángulo A4” en la referencia a tamaño del papel A4 definida ya en el ISO 216.

Referencias

↑ Table of silver means

Explicación del significado de la razón plateada

Categorías:

Constantes matemáticas
Números irracionales

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Número áureo — Para el número de astronomía, ver Número áureo (astronomía) El número áureo o de oro (también llamado número plateado, razón extrema y media,[1] razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) representado por la… … Wikipedia Español
Foxy el Zorro Plateado — Saltar a navegación, búsqueda Foxy el Zorro Plateado Gin gitsune no Fokushī Sexo Masculino Edad ? One Piece … Wikipedia Español
Power Rangers R.P.M — Saltar a navegación, búsqueda Power Rangers RPM Género Acción aventura, Drama Reparto Eka Darville Ari Boyland Rose McIver Milo Cawthorne Daniel Ewing Mike Ginn Li Ming Hu Olivia Tennet James Gaylyn Adelaide Kane Voces de Andrew Laing Mark… … Wikipedia Español
Cerebros de la Frontera — Anexo:Cerebros de la Frontera Saltar a navegación, búsqueda Los Cerebros de la Batalla de la Frontera, son un grupo ficticio del anime, manga y los juegos Pokémon. Son poderosos entrenadores pokémon y cada uno de estos Cerebros Frontera, se… … Wikipedia Español
Tecnecio — «Tc» redirige aquí. Para otras acepciones, véase TC. Molibdeno ← Tecnecio → Rutenio Mn … Wikipedia Español
Criaturas en Harry Potter — Anexo:Criaturas en Harry Potter Saltar a navegación, búsqueda La serie de libros sobre el mago Harry Potter contiene un gran número de animales fantásticos y plantas mágicas algunas inventadas por J.K. Rowling y otras criaturas mitológicas que… … Wikipedia Español
Aditivos alimentarios — Anexo:Aditivos alimentarios Saltar a navegación, búsqueda Esta es la lista que contiene todos los aditivos para los alimentos, permitidos por la UE. En esta tabla deberían estar todos, incluso los cancerígenos, los bioperjudiciales, y los que… … Wikipedia Español
Semana Santa en El Puerto de Santa María — Este artículo o sección sobre religión y sociedad necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 10 de marzo de 2009. Ta … Wikipedia Español
Anexo:Criaturas en Harry Potter — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Semana Santa en Roquetas de Mar — La Semana Santa en Roquetas de Mar es una de las celebraciones más importantes del municipio de Roquetas de Mar, en la provincia de Almería, en Andalucía (España). En Roquetas de Mar centro y sus barrios más próximos (Doscientas Viviendas y El… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Número plateado

Contenido