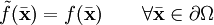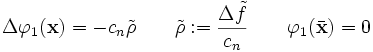Ecuación de Poisson

Ecuación de Poisson

Ecuación de Poisson

En matemática y física, la ecuación de Poisson es una ecuación en derivadas parciales con una amplia utilidad en electrostática, ingeniería mecánica y física teórica. Su nombre se lo debe al matemático, geómetra y físico francés Siméon-Denis Poisson.

La ecuación de Poisson se define como:

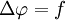
\Delta \varphi = f

donde 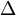\Delta\; es el operador laplaciano, y f y φ son funciones reales o complejas. En un sistema de coordenadas cartesianas tridimensional, toma la forma:

\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right)\varphi(x,y,z) = f(x,y,z).

Si f = 0, la ecuación se convierte en la ecuación de Laplace

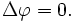
\Delta \varphi = 0. \!

Contenido

Problema de Poisson

La ecuación de Poisson junto con las condiciones de contorno homogéneas, constituye uno de los tres problemas clásicos relacionados con el operador laplaciano que se detallan a continuación. Concretamente el problema de Poisson es el problema de encontrar una función definida sobre el dominio Ω que satisfaga:

(1) \begin{cases} \Delta \varphi(\mathbf{x}) = -c_n\rho(\mathbf{x}) & \mathbf{x} \in \Omega \subset \R^n \\ \varphi(\bar\mathbf{x}) = 0 & \bar\mathbf{x} \in \partial \Omega \end{cases}

Este tipo de problema puede ser resuelto de manera sencilla, mediante el método de la función de Green, para n > 2:

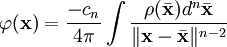
\varphi(\mathbf{x}) = \frac{-c_n}{4\pi} \int \frac{\rho(\bar\mathbf{x})d^n\bar\mathbf{x}}{\|\mathbf{x}-\bar\mathbf{x}\|^{n-2}}

Problemas de potencial

La ecuación anterior aparece en problemas electrostáticos y de potencial gravitatorio. En esos problemas ρ representa la densidad de carga eléctrica o bien la densidad de masa. Además la constante cn debe ser tomada 1/ε0 para problemas electrostáticos (en SI), mientras que en problemas de potencial gravitatorio se toma como cn = 4πG.

Problema de Dirichlet

Artículo principal: Problema de Dirichlet

El problema de Dirichlet es un problema de encontrar una función armónica sobre un dominio tal que sea igual a otra función dada sobre el contorno del dominio:

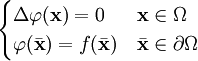
(2) \begin{cases} \Delta \varphi(\mathbf{x}) = 0 & \mathbf{x} \in \Omega \\ \varphi(\bar\mathbf{x}) = f(\bar\mathbf{x}) & \bar\mathbf{x} \in \partial \Omega \end{cases}

En electrostática el problema de Dirichlet se corresponde con el problema de encontrar el campo dentro de una cavidad metálica "conectada a tierra" (potencial constante) de forma Ω dentro de la cual hay una distribución de carga dada por ρ.

Relación con el problema de Poisson

Existe un medio para reducir el problema de Dirichlet a un problema de Poisson. Si 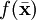f(\bar\mathbf{x}) es una función de clase C1 sobre la frontera del dominio y 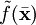\tilde{f}(\bar\mathbf{x}) es una extensión de f a todo el dominio Ω que sea de clase C2, es decir:

\tilde{f}(\bar\mathbf{x}) = f(\bar\mathbf{x}) \qquad \forall \bar\mathbf{x} \in \partial \Omega


Entonces la solución del problema de Dirichlet (2) viene dada por una función suma de la extensión anterior y otra función que es solución de un problema de Poisson como (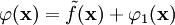1):

\varphi(\mathbf{x}) = \tilde{f}(\mathbf{x}) + \varphi_1(\mathbf{x})

\Delta \varphi_1(\mathbf{x}) = -c_n\tilde{\rho} \qquad \tilde{\rho}:= \frac{\Delta \tilde{f}}{c_n} \qquad \varphi_1(\bar\mathbf{x})=0

Problema de Von Neumann

El problema de Von Neumann es similar al anterior pero en lugar de fijar el valor de la función incógnita sobre la frontera, fija el valor de la derivada perpendicularmente a la superficie.

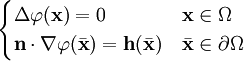
(3) \begin{cases} \Delta \varphi(\mathbf{x}) = 0 & \mathbf{x} \in \Omega \\ \mathbf{n} \cdot \nabla\varphi(\bar\mathbf{x}) = \mathbf{h}(\bar\mathbf{x}) & \bar\mathbf{x} \in \partial \Omega \end{cases}

Referencias

Enlaces externos

Obtenido de "Ecuaci%C3%B3n de Poisson"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Ecuación de Poisson-Boltzmann — La ecuación de Poisson Boltzmann es una ecuación diferencial que describe interacciones electrostáticas entre moléculas en soluciones iónicas. Es la base matemática para el modelo de la Doble Capa Eléctrica Interfacial de Gouy Chapman, propuesta… …   Wikipedia Español

  • Aplicación de la ecuación de Poisson en macromoléculas — Saltar a navegación, búsqueda En el estudio de las macromoléculas es posible hacer uso de ecuaciones utilizadas habitualmente en la dinámica de fluidos o en el electromagnetismo; una de estas es la ecuación de Poisson, que es posible obtener a… …   Wikipedia Español

  • La ecuación de Poisson-Boltzmann — Saltar a navegación, búsqueda Este modelo considera que el potencial químico es uniforme en toda la solución de iones, es decir, no se considera explícitamente cada ion. Las contribuciones electrostáticas y entrópicas del potencial químico de un… …   Wikipedia Español

  • Ecuación de Laplace — Saltar a navegación, búsqueda En cálculo vectorial, la ecuación de Laplace es una ecuación en derivadas parciales de segundo orden de tipo elíptico, que recibe ese nombre en honor al físico y matemático Pierre Simon Laplace. Introducida por las… …   Wikipedia Español

  • Ecuación del campo de Einstein — Saltar a navegación, búsqueda En física, la ecuación del campo de Einstein o la ecuación de Einstein es una ecuación en la teoría de la gravitación, llamada relatividad general, que describe cómo la materia crea gravedad e, inversamente, cómo la… …   Wikipedia Español

  • Ecuación de Debye-Huckel — Saltar a navegación, búsqueda Peter Debye y Erich Hückel plantearon un modelo que describe una mezcla de iones (electrolitos), inmersos en un medio dieléctrico continuo de temperatura T, presión P y concentración molar ci, , en donde los iones de …   Wikipedia Español

  • Ecuación elíptica en derivadas parciales — Saltar a navegación, búsqueda Una ecuación eliptica en derivadas parciales de segundo orden es una ecuación diferencial parcial del tipo en la cual la matriz es definida positiva. Un ejemplo de una ecuación diferencial parcial elíptica es la… …   Wikipedia Español

  • Ecuación de Schrödinger — Saltar a navegación, búsqueda La ecuación de Schrödinger fue desarrollada por el físico austríaco Erwin Schrödinger en 1925. Describe la evolución temporal de una partícula masiva no relativista. Es de importancia central en la teoría de la… …   Wikipedia Español

  • Poisson — Poisson, Simeon Denis Poisson, ecuación de …   Enciclopedia Universal

  • Poisson, ecuación de — ► FÍSICA Generalización de la ecuación de Laplace para el potencial gravitatorio o el potencial eléctrico que los relaciona phiv (x, y, z) con la distribución espacial de masas (o cargas) cuya densidad en el punto (x, y, z) está dada por ρ (x, y …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”