La ecuación de Saha nos indica los estados de ionización de un átomo, es también conocida como ecuación de fotoionización y es una de las 4 ecuaciones básicas del equilibrio termodinámico.

Introducción

Segun la teoria atomica, el número de especies de un átomo depende de la cantidad de su numero de protones, el hidrógeno al contar con un solo protón tiene dos especies (HI y HII), el helio que tiene dos protones cuenta con tres especies: HeI (neutro), HeII (una vez ionizado) y HeIII (helio dos veces ionizado).

La ecuación de Saha calcula la cantidad de especies a partir de la densidad, la temperatura y la composición química de un gas. Utiliza la suposición de equilibrio termodinámico y toma en cuenta las interacciones fotón-partícula, no toma en cuenta las interacciones por choques. Por lo tanto, calcula la cantidad de electrones libres en el sistema.

Idea física

Un gas compuesto por diversos átomos: hidrógeno, helio, carbono, etc. se encuentran a cierta temperatura T, cada átomo tiene a su vez electrones en diferentes niveles cuánticos. Cuando el sistema se encuentra en equilibrio, la cantidad de electrones que caen en el potencial de un átomo es igual a la cantidad de electrones que son expulsados del potencial atómico.

La tasa de interacción electrón-ion depende de la distribución de velocidades de Maxwell mientras que las poblaciones de niveles energéticos de cada especie depende de la Ecuación de Boltzmann, este par de ecuaciones depende de la temperatura del sistema y debido a la suposición de equilibrio termodinamico las temperaturas son iguales.

Al poblar los niveles energéticos con la distribución de Boltzmann y calcular la tasa de interacción de electrones proveniente de la distribución de velocidades de Maxwell llegamos a la ecuación de Saha.

Calculando especies con la ecuación de Saha

Como vimos, la ecuación de Saha nos dice la cantidad de especies y de electrones de nuestro sistema. Para resolver numéricamente tenemos que la ecuación de Saha se puede escribir como

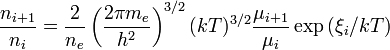
donde n_{i + 1} es la densidad numérica de la especie "i+1", n_i es la densidad numérica de la especie "i", n_e es la densidad numérica de electrones, m_e es la masa del electrón en eV, h es la constante de Planck, k es la constante de Boltzmann, T es la temperatura en Kelvin, μ_i es la función de partición para la misma especie "i", ξ_i es la energía de ionización de la especie "i" también en eV.

Tomando los valores correspondientes, la ecuación de Saha puede reducirse a una manera practica

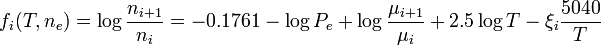
donde P_e es la presión electrónica de un gas ideal
P_e = n_eKT

Calculando especies de un gas de Hidrógeno-Helio

Para calcular las especies de un gas de Hidrógeno-Helio (HI, HII, HeI, HeII, HeIII, n_e) se tiene que cumplir el siguiente conjunto de ecuaciones



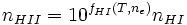
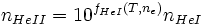
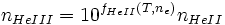
n_HI + n_HII = n_H
n_HeI + n_HeII + n_HeIII = n_He
n_HII + n_HeII + 2n_HeIII = n_e
donde f_i(T,n_e) es la ecuación de Saha para la especie "i", n_H es el hidrogeno total y n_He es el Helio total.

Este conjunto de ecuaciones se resuelve simultáneamente y de manera iterativa hasta que la densidad electrónica permanece constante, lo que indica que el equilibrio de fotoionización se ha establecido.