Ecuación de Schrödinger

Ecuación de Schrödinger: Ecuación de Schrödinger

Saltar a navegación, búsqueda

La ecuación de Schrödinger fue desarrollada por el físico austríaco Erwin Schrödinger en 1925. Describe la evolución temporal de una partícula masiva no relativista. Es de importancia central en la teoría de la mecánica cuántica, donde representa para las partículas microscópicas un papel análogo a la segunda ley de Newton en la mecánica clásica. Las partículas microscópicas incluyen a las partículas elementales, tales como electrones, así como sistemas de partículas, tales como núcleos atómicos.

Contenido

1 Nacimiento de la ecuación

1.1 Contexto histórico

1.2 La derivación histórica

2 Interpretación estadística de la función de onda

3 Formulación moderna de la ecuación

3.1 Limitaciones de la ecuación

4 Resolución de la ecuación

4.1 Búsqueda de los estados propios

4.2 Rareza de una solución analítica exacta

5 Límite clásico de la ecuación de Schrödinger

6 Formulacion Matricial

7 Bibliografía

8 Notas

Nacimiento de la ecuación

Contexto histórico

Al comienzo del siglo XX se había comprobado que la luz presentaba una dualidad onda corpúsculo, es decir, la luz se podía manifestar según las circunstancias como partícula (fotón en el efecto fotoeléctrico), o como onda electromagnética en la interferencia luminosa. En 1923 Louis-Victor de Broglie propuso generalizar esta dualidad a todas las partículas conocidas. Propuso la hipótesis, paradójica en su momento, de que a toda partícula clásica microscópica se le puede asignar una onda, lo cual se comprobó experimentalmente en 1927 cuando se observó la difracción de electrones. Por analogía con los fotones, De Broglie asocia a cada partícula libre con energía $E$ y cantidad de movimiento $p$ una frecuencia $ν$ y una longitud de onda $λ$ :

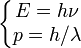
$\left\{\begin{matrix}E=h\nu\\p=h/\lambda\end{matrix}\right.$

La comprobación experimental hecha por Clinton Davisson y Lester Germer mostró que la longitud de onda asociada a los electrones medida en la difracción según la fórmula de Bragg se correspondía con la longitud de onda predicha por la fórmula de De Broglie.

Esa predicción llevó a Schrödinger a tratar de escribir una ecuación para la onda asociada de De Broglie que para escalas macroscópicas se redujera a la ecuación de la mecánica clásica de la partícula. La energía mecánica total clásica es:

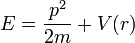
$E = {p^2\over 2m}+ V(r)$

El éxito de la ecuación, deducida de esta expresión utilizando el principio de correspondencia, fue inmediato por la evaluación de los niveles cuantificados de energía del electrón en el átomo de hidrógeno, pues ello permitía explicar el espectro de emisión del hidrógeno: series de Lyman, Balmer, Bracket, Paschen, Pfund, etc.

La interpretación física correcta de la función de onda de Schrödinger fue dada en 1926 por Max Born. En razón del carácter probabilista que se introducía, la mecánica ondulatoria de Schrödinger suscitó inicialmente la desconfianza de algunos físicos de renombre como Albert Einstein, para quien «Dios no juega a los dados».

La derivación histórica

El esquema conceptual utilizado por Schrödinger para derivar su ecuación reposa sobre una analogía formal entre la óptica y la mecánica:

En la óptica ondulatoria, la ecuación de propagación en un medio transparente de índice real n variando lentamente a la escala de la longitud de onda conduce —mientras se busca una solución monocromática donde la amplitud varía muy lentamente ante la fase— a una ecuación aproximada denominada eikonal. Es la aproximación de la óptica geométrica, a la cual está asociada el principio variacional de Fermat.

En la formulación hamiltoniana de la mecánica clásica, existe una ecuación de Hamilton-Jacobi (que en última instancia es equivalente a las leyes de Newton). Para una partícula masiva no relativista sometida a una fuerza que deriva de una energía potencial, la energía mecánica total es constante y la ecuación de Hamilton-Jacobi para la ”función característica de Hamilton” se parece formalmente a la ecuación de la eikonal (el principio variacional asociado es el principio de mínima acción.)

Este paralelismo lo había notado ya Hamilton en 1834, pero el no tenía una razón para dudar de la validez de la mecánica clásica. Después de la hipótesis de de Broglie de 1923, Schrödinger dice:^[1] la ecuación de la eikonal siendo una aproximación a la ecuación de onda de la óptica ondulatoria, buscamos la ecuación de onda de la "mecánica ondulatoria" (a realizar) donde la aproximación será la ecuación de Hamilton-Jacobi. Lo que falta, primero para una onda estacionaria (E = cte), después para una onda de cualquier tipo.^[2]

Schrödinger había en efecto comenzado por tratar el caso de una partícula relativista —como de Broglie antes que él—.^[3] Entonces había obtenido la ecuación conocida hoy día con el nombre de Klein-Gordon, pero su aplicación al caso del potencial eléctrico del átomo de hidrógeno daba unos niveles de energía incompatibles con los resultados experimentales.^[4] Ello hará que se concentre sobre el caso no-relativista, con el éxito conocido.

Derivación elemental

Una vez establecida el paralelismo entre la óptica y la mecánica hamiltoniana, la parte no trivial del razonamiento, la derivación de la ecuación es algo relativamente elemental. En efecto, la ecuación de onda satisfecha por la amplitud espacial de una onda monocromática estática de pulsación $ω$ fija en un medio de índice n que varía lentamente se escribe como:

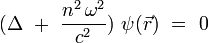
$(\Delta \ + \ \frac{n^2 \, \omega^2}{c^2}) \ \psi(\vec{r}) \ = \ 0$

Introducimos el número de ondas k dentro del medio de índice n, tal como :

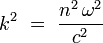
$k^2 \ = \ \frac{n^2 \, \omega^2}{c^2}$

Se obtiene entonces la ecuación de Helmholtz:

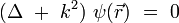
$(\Delta \ + \ k^2) \ \psi(\vec{r}) \ = \ 0$

La longitud de onda dentro del medio está definida por : $λ = 2π / k$ . La ecuación de Helmholtz se reescribe :

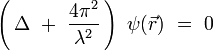
$\left( \, \Delta \ + \ \frac{4\pi^2}{\lambda^2} \, \right) \ \psi(\vec{r}) \ = \ 0$

Se utiliza entonces la relación de de Broglie para una partícula non-relativista, para la cual la cantidad de movimiento p = m v :

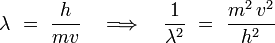
$\lambda \ = \ \frac{h}{mv} \quad \Longrightarrow \quad \frac{1}{\lambda^2} \ = \ \frac{m^2 \, v^2}{h^2}$

O, la energía cinética se escribe para una partícula no-relativista :

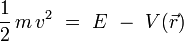
$\frac{1}{2} \, m \, v^2 \ = \ E \ - \ V(\vec{r})$

de donde la ecuación de Schrödinger estacionaria :

$\left[ \, \Delta \ + \ \frac{8\pi^2m}{h^2} \, \left( \, E \ - \ V(\vec{r}) \, \right) \ \right] \ \psi(\vec{r}) \ = \ 0$

Introduciendo el cuanto de acción 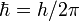$\hbar = h/2\pi$ , la ponemos en la forma habitual :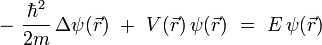

$- \ \frac{\hbar^2}{2m} \, \Delta \psi(\vec{r}) \ + \ V(\vec{r}) \, \psi(\vec{r}) \ = \ E \, \psi(\vec{r})$

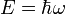Solo resta reintroducir el tiempo t explicitando la dependencia temporal para una onda monocromática, puesto que utilizando la relación de Planck-Einstein $E = \hbar \omega$ :

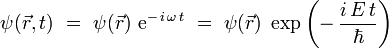
$\psi(\vec{r},t) \ = \ \psi(\vec{r}) \ \mathrm{e}^{- \, i \, \omega \, t} \ = \ \psi(\vec{r}) \ \exp \left( - \, \frac{i \, E \, t}{\hbar} \right)$

Se obtiene finalmente la ecuación de Schrödinger general :

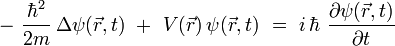
$- \ \frac{\hbar^2}{2m} \, \Delta \psi(\vec{r},t) \ + \ V(\vec{r}) \, \psi(\vec{r},t) \ = \ i \, \hbar \ \frac{\partial \psi(\vec{r},t)}{\partial t}$

Interpretación estadística de la función de onda

A principios de la década de 1930 Max Born que había trabajado junto con Werner Heisenberg y Pascual Jordan en una versión de la mecánica cuántica basada en el formalismo matricial alternativa a la de Heisenberg apreció que la ecuación de Schrödinger compleja tiene una integral de movimiento dada por ψ*(x)ψ(x) (= |ψ(x)|²) que podía ser interpretada como una densidad de probabilidad. Born le dio a la función de onda una interpretación probabilística diferente de la que De Broglie y Schrödinger le habían dado, y por ese trabajo recibió el premio Nobel en 1954. Born ya había apreciado en su trabajo mediante el formalismo matricial de la mecánica cuántica que el conjunto de estados cuánticos llevaba de manera natural a construir espacios de Hilbert para representar los estados físicos de un sistema cuántico.

De ese modo se abandonó el enfoque de la función de onda como una onda material, y pasó a interpretarse de modo más abstracto como una amplitud de probabilidad. En la moderna mecánica cuántica, el conjunto de todos los estados posibles en un sistema se describe por un espacio de Hilbert complejo y separable, y cualquier estado instantáneo de un sistema se describe por un "vector unitario" en ese espacio (o más bien una clase de equivalencia de vectores unitarios). Este "vector unitario" codifica las probabilidades de los resultados de todas las posibles medidas hechas al sistema. Como el estado del sistema generalmente cambia con el tiempo, el vector estado es una función del tiempo. Sin embargo, debe recordarse que los valores de un vector de estado son diferentes para distintas localizaciones, en otras palabras, también es una función de x (o, tridimensionalmente, de r). La ecuación de Schrödinger da una descripción cuantitativa de la tasa de cambio en el vector estado.

Formulación moderna de la ecuación

En mecánica cuántica, el estado en el instante t de un sistema se describe por un elemento 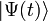$\left| \Psi (t)\right\rangle$ del espacio complejo de Hilbert — usando la notación bra-ket de Paul Dirac. 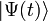$\left| \Psi (t)\right\rangle$ representa las probabilidades de resultados de todas las medidas posibles de un sistema.

La evolución temporal de 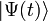$\left| \Psi (t)\right\rangle$ se describe por la ecuación de Schrödinger :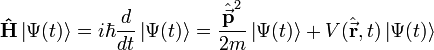

$\mathbf{\hat{H}} \left| \Psi (t)\right\rangle = i \hbar {d\over dt} \left| \Psi (t) \right\rangle = \frac{\hat{\vec{\mathbf{p}}}^2}{2m}\left| \Psi (t)\right\rangle + V(\hat{\vec{\mathbf{r}}},t)\left| \Psi (t) \right\rangle$

donde

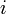$i\,$ : es la unidad imaginaria ;

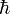$\hbar\,$ : es la constante de Planck normalizada (h/2π) ;

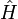$\hat{H}\,$ : es el hamiltoniano, dependiente del tiempo en general, el observable corresponde a la energía total del sistema ;

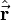$\hat{\vec{\mathbf{r}}}\,$ : es el observable posición ;

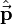$\hat{\vec{\mathbf{p}}}\,$ : es el observable impulso.

Como con la fuerza en la segunda ley de Newton, su forma exacta no la da la ecuación de Schrödinger, y ha de ser determinada independientemente, a partir de las propiedades físicas del sistema cuántico.

Debe notarse que, contrariamente a las ecuaciones de Maxwell que describen la evolución de las ondas electromagnéticas, la ecuación de Schrödinger es no relativista. Nótese también que esta ecuación no se demuestra: es un postulado. Se supone correcta después de que Davisson y Germer hubieron confirmado experimentalmente la hipotesis de Louis de Broglie.

Para más información del papel de los operadores en mecánica cuántica, véase la formulación matemática de la mecánica cuántica.

Limitaciones de la ecuación

La ecuación de Schrödinger es una ecuación no relativista que sólo puede describir partículas cuyo momento lineal sea pequeño comparada con la energía en reposo dividida de la velocidad de la luz.

Además la ecuación de Schrödinger no incorpora el espín de las partículas adecuadamente. Pauli generalizó ligeramente la ecuación de Schrödinger al introducir en ella términos que predecían correctamente el efecto del espín, la ecuación resultante es la ecuación de Pauli.

Más tarde Dirac, proporcionó la ahora llamada ecuación de Dirac que no sólo incorporaba el espín para fermiones de espín 1/2, sino que introducía los efectos relativistas

Resolución de la ecuación

La ecuación de Schrödinger, al ser una ecuación vectorial, se puede reescribir de manera equivalente en una base particular del espacio de estados. Si se elige por ejemplo la base 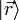$\left|\vec{r}\right\rangle$ correspondiente a la representación de posición definida por: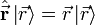

$\hat{\vec{\mathbf{r}}}\left|\vec{r}\right\rangle=\vec{r}\left|\vec{r}\right\rangle$

Entonces la función de onda 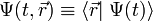$\Psi (t,\vec{r})\equiv\left\langle\vec{r}\right|\left.\Psi(t)\right\rangle\,$ satisface la ecuación siguiente: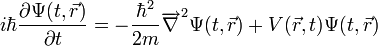

$i\hbar{\partial\Psi(t,\vec{r})\over\partial t}=-{\hbar^2\over 2m}\overrightarrow{\nabla}^2\Psi(t,\vec{r})+V(\vec{r},t)\Psi(t,\vec{r})$

Donde 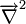$\overrightarrow{\nabla}^2\,$ es el laplaciano.

De esta forma se ve que la ecuación de Schrödinger es una ecuación en derivadas parciales en la que intervienen operadores lineales, lo cual permite escribir la solución genérica como suma de soluciones particulares. La ecuación es en la gran mayoría de los casos demasiado complicada para admitir una solución analítica de forma que su resolución se hace de manera aproximada y/o numérica.

Búsqueda de los estados propios

Los operadores que aparecen en la ecuación de Schrödinger son operadores lineales; de lo que se deduce que toda combinación lineal de soluciones es solución de la ecuación. Esto lleva a favorecer la búsqueda de soluciones que tengan un gran interés teórico y práctico: a saber los estados que son propios del operador hamiltoniano. Estos estados, denominados estados estacionarios, son las soluciones de la ecuación de estados y valores propios,

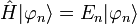
$\hat{H}|\varphi_{n}\rangle =E_{n}|\varphi_{n}\rangle$

denominada habitualmente ecuación de Schrödinger independiente del tiempo. El estado propio 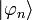$|\varphi_{n}\rangle$ está asociado al valor propio $E n$ , escalar real que corresponde con la energía de la partícula en dicho estado.

Los valores de la energía pueden ser discretos como las soluciones ligadas a un pozo de potencial (por ejemplo nivel del átomo de hidrógeno); resultando una cuantificación de los niveles de energía. Estas pueden corresponder también a un espectro continuo como las soluciones libres de un pozo de potencial (por ejemplo un electrón que tenga la suficiente energía para alejarse al infinito del núcleo de átomo de hidrógeno).

A menudo se obtiene que numerosos estados 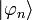$|\varphi_{n}\rangle$ corresponden a un mismo valor de la energía: hablamos entonces de niveles de energía degenerados.

De manera general, la determinación de cada uno de los estados propios del hamiltoniano, 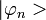$|\varphi_{n}>$ , y de la energía asociada, da el estado estacionario correspondiente, solución de la ecuación de Schrödinger :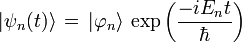

$|\psi_{n}(t)\rangle \,= \, |\varphi_{n}\rangle \, \exp\left( \frac{-iE_{n}t}{\hbar} \right)$

Una solución de la ecuación de Schrödinger puede entonces escribirse generalmente como una combinación lineal de tales estados:

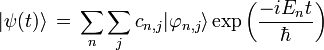
$|\psi(t)\rangle \, = \, \sum_{n}\sum_{j} c_{n,j}|\varphi_{n,j}\rangle \exp \left( \frac{-iE_{n}t}{\hbar} \right)$

Según los postulados de la mecánica cuántica,

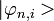el escalar complejo $c n, i$ es la amplitud del estado $| ψ(t) >$ sobre el estado $|\varphi_{n,i}>$ ;

el real $Σ i | c n, i | 2$ es la probabilidad (en el caso de un espectro discreto) de encontrar la energía $E n$ mientras se hace una medida de la energía sobre el sistema.

Rareza de una solución analítica exacta

La búsqueda de estados propios del hamiltoniano es en general compleja. Incluso en el caso resoluble analíticamente del átomo de hidrógeno solo es rigurosamente resoluble de forma simple si se descarta el acoplamiento con el campo electromagnético que permite el paso a los estados excitados, soluciones de la ecuación de Schrödinger del átomo, desde el nivel fundamental.

Algunos modelos simples, aunque no del todo conformes con la realidad, pueden ser resueltos analíticamente y son muy útiles. Estas soluciones sirven para entender mejor la naturaleza de los fenómenos cuánticos, y en ocasiones son una aproximación razonable al comportamiento de sistemas más complejos (en mecánica estadística se aproximan las vibraciones moleculares como osciladores armónicos). Ejemplos de modelos:

La partícula libre (potencial nulo) ;

La partícula en una caja

Un haz de partícula incidiendo sobre una barrera de potencial

La partícula en un anillo

La partícula en un potencial de simetría esférica

El oscilador armónico cuántico (potencial cuadrático)

El átomo de hidrógeno (potencial de simetría esférica)

La partícula en una red monodimensional (potencial periódico)

En los otros casos, hay que usar técnicas de aproximación :

La teoría perturbacional da expresiones analíticas en la forma de desarrollos asintóticos alrededor de un problema sin-perturbaciones que sea resoluble exactamente.

El análisis numérico permite explorar casos inaccesibles a la teoría de perturbaciones.

El método variacional

Las soluciones de Hartree-Fock

Los métodos cuánticos de Monte Carlo

Límite clásico de la ecuación de Schrödinger

Inicialmente la ecuación de Schrödinger se consideró simplemente como la ecuación de movimiento de un campo material que se propagaba en forma de onda. De hecho puede verse que en el límite clásico, cuando 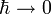$\hbar \to 0$ la ecuación de Schrödinger se reduce a la ecuación clásica de movimiento en términos de acción o ecuación de Hamilton-Jacobi. Para ver esto, trabajaremos con la función de onda típica que satisfaga la ecuación de Schrödinger dependiente del tiempo que tenga la forma: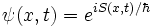

$\psi(x,t) = e^{iS(x,t)/\hbar}$

Donde 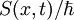$S(x,t)/\hbar$ es la fase de la onda si substituimos esta solución en la ecuación de Schrödinger dependiente del tiempo después de un poco de álgebra llegamos a que:

(4) $\frac{\partial S}{\partial t}+\frac{1}{2m}\left[\left(\frac{\partial S}{\partial x}\right)^2 + \left(\frac{\partial S}{\partial y}\right)^2 + \left(\frac{\partial S}{\partial z}\right)^2 \right] + V(x) = \frac{i\hbar}{2m} \Delta S$

Si se toma el límite 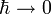$\hbar \to 0$ el segundo miembro desaparece y tenemos que la fase de la función de onda coincide con la magnitud de acción y esta magnitud puede tomarse como real. Igualmente puesto que la magnitud de acción es proporcional a la masa de una partícula 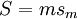$S = m s_m \,$ puede verse que para partículas de masa grande el segundo miembro es mucho más pequeño que el primero:

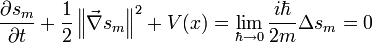
(5) $\frac{\partial s_m}{\partial t}+\frac{1}{2}\left\Vert \vec\nabla s_m \right\Vert^2 + V(x) = \lim_{\hbar \to 0} \frac{i\hbar}{2m} \Delta s_m = 0$

Y por tanto para partículas macroscópicas, dada la pequeñez de la constante de Planck, los efectos cuánticos resumidos en el segundo miembro se anulan, lo cual explica porqué los efectos cuánticos sólo son apreciables a escalas subatómicas.

De acuerdo con el principio de correspondencia las partículas clásicas de gran masa, comparada con la escala cuántica, son partículas localizadas describibles mediante un paquete de ondas altamente localizado que se desplaza por el espacio. La longitud de onda de dicha de las ondas que conformaban dicho paquete material están en torno a la longitud de De Broglie para la partícula, y la velocidad de grupo del paquete coincide con la velocidad del movimiento de la partícula lo que reconcilia la naturaleza corpuscular observada en ciertos experimentos con la naturaleza ondulatoria observada para partículas subatómicas.

Formulacion Matricial

Existe una formulación matricial de la mecánica cuántica, en dicha formulación existe una ecuación cuya forma es esencialmente la misma que la de las ecuaciones clásicas del movimiento, dicha ecuación es

(6) $\frac{\text{d} \hat A}{\text{d} t} \, = \, \frac{\partial \hat A}{\partial t}-\frac{i}{\hslash}[\hat A, \, \hat H]$

De esta ecuación es posible deducir la segunda ley de Newton, resolviendo para el operador 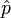$\hat p$ . En efecto se tiene

(7) $\frac{\text{d} \hat p}{\text{d} t} \, = \, -\frac{i}{\hslash} [\hat p, \, \hat H]$

evaluando el conmutador se deduce

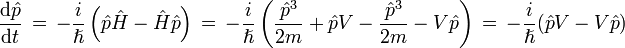
(8) $\frac{\text{d} \hat p}{\text{d} t} \, = \, -\frac{i}{\hslash} \left( \hat p \hat H - \hat H \hat p \right) \, = \, -\frac{i}{\hslash}\left(\frac{\hat{p}^3}{2 m} + \hat p V - \frac{\hat{p}^3}{2 m} - V \hat p\right) \, = \, -\frac{i}{\hslash}(\hat p V - V \hat p)$

No es dificil demostrar que 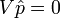$V \hat p = 0$ y, por tanto, se obtiene

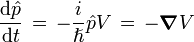
(9) $\frac{\text{d} \hat p}{\text{d} t} \, = \, -\frac{i}{\hslash} \hat p V \, = \, - \boldsymbol{\nabla} V$

donde se ha usado 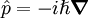$\hat p = - i \hslash \boldsymbol{\nabla}$ . Este resultado es análogo al de la mecánica clásica, para una ecuación parecida que involucra los corchetes de Poisson, más aun, esta ecuación es justamente la formulación Newtoniana de la mecánica.

Bibliografía

Erwin Schrödinger; Mémoires sur la mécanique ondulatoire, Félix-Alcan (París-1933). Reedición Jacques Gabay (1988), ISBN 2-87647-048-9. Contiene la traducción al francés de Alexandre Proca de las memorias históricas de 1926 :

Cuantificación y valores propios (I) y (II), Annalen der Physik (4) 79 (1926) [[1]] y [[2]] (en alemán);

Sobre la comparación entre la mecánica cuántica de Heisenberg-Born-Jordan y la mía, Annalen der Physik (4) 79 (1926) [[3]] (en alemán);

Cuantificación y valores propios (III) - Teoría de las perturbaciones con aplicación del efecto Stark a las rayas de Balmer, Annalen der Physik (4) 80 (1926) [[4]] (en alemán);

Cuantificación y valores propios (IV), Annalen der Physik (4) 81 (1926) [[5]] (en alemán);

Sobre el efecto Compton, Annalen der Physik (4) 82(1927) [[6]] (en alemán);

El teorema de la conservación de la energía y la cantidad de movimiento para las ondas materiales, Annalen der Physik (4) 82 (1927) [[7]] (en alemán);

Intercambios de energía según la mecánica ondulatoria, Annalen der Physik (4) 83 (1927)[[8]] (en alemán).

Erwin Schrödinger, «An Undulatory Theory of the Mechanics of Atoms and Molecules», Phys. Rev. 28, 1049 (1926) [[9]] (en inglés)

Notas

↑ Schrödinger discute en detalle las relaciones entre la mecánica hamiltoniana y la óptica en 1926 (véase bibliografía). Walter Moore; Schrödinger - Life & Thought, Cambridge University Press (1989).

↑ Para los curiosos, esta derivación se detalla en: Herbert Goldstein; Classical mechanics, Addison-Wesley (2×10^{{{1}}} edición-1980), párrafo 10.8, pp. 484-492.

↑ Abraham Païs; Inward Bound, Oxford University Press (1986).

↑ La fórmula de Balmer obtenida es correcta, pero la estructura fina es incorrecta.

Obtenido de "Ecuaci%C3%B3n de Schr%C3%B6dinger"

Categorías: Ecuaciones | Mecánica cuántica | Química cuántica

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

Ecuación de Schrödinger — La ecuación de Schrödinger, desarrollada por el físico austríaco Erwin Rudolf Josef Alexander Schrödinger en 1925, describe la dependencia temporal de los sistemas mecanocuánticos. Es de importancia central en la teoría de la mecánica cuántica,… … Enciclopedia Universal
Ecuación de Schrödinger-Pauli — Saltar a navegación, búsqueda La ecuación de Pauli o ecuación de Schrödinger Pauli, es una generalización o reformulzación de la ecuación de Schrödinger para partículas de espín 1/2 que tiene en cuenta la interacción entre el espín y el campo… … Wikipedia Español
Ecuación de Dirac — Saltar a navegación, búsqueda La ecuación de Dirac de ondas relativista de la mecánica cuántica fue formulada por Paul Dirac en 1928. Da una descripción de las partículas elementales de espín ½, como el electrón, y es completamente consistente… … Wikipedia Español
Ecuación de Hamilton-Jacobi — Saltar a navegación, búsqueda La ecuación de Hamilton Jacobi es una ecuación diferencial en derivadas parciales usada en mecánica clásica y mecánica relativista que permite encontrar las ecuaciones de evolución temporal o de movimiento . La… … Wikipedia Español
Ecuación de Klein-Gordon — Saltar a navegación, búsqueda La ecuación de Klein Gordon o ecuación K G debe su nombre a Oskar Klein y Walter Gordon, y es la ecuación que describe un campo escalar libre en teoría cuántica de campos. Contenido 1 Historia 2 Forma de la ecuación … Wikipedia Español
Ecuación de onda — Saltar a navegación, búsqueda La ecuación de onda es una importante ecuación diferencial parcial lineal de segundo orden que describe la propagación de una variedad de ondas, como las ondas sonoras, las ondas de luz y las ondas en el agua. Es… … Wikipedia Español
Ecuación de movimiento — Saltar a navegación, búsqueda En física, una ecuación de movimiento es una ecuación diferencial que caracteriza cómo es la evolución temporal de un sistema físico. Esta ecuación relaciona la derivada temporal de una o varias variables que… … Wikipedia Español
Ecuación de continuidad — Saltar a navegación, búsqueda En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial. Contenido 1 Teoría Electromagnética 2 Mecánica de fluidos … Wikipedia Español
Ecuación de Langevin — Saltar a navegación, búsqueda En física estadística, una ecuación de Langevin es una ecuación diferencial estocástica que describe el movimiento browniano en un potencial. Las primeras ecuaciones de Langevin que fueron estudiadas fueron aquellas… … Wikipedia Español
Ecuación parabólica en derivadas parciales — Saltar a navegación, búsqueda Una ecuación parabólica en derivadas parciales es una ecuación diferencial parcial de segundo orden del tipo en la cual la matriz tiene un determinante igual a 0. Algunos ejemplo de ecuaciones diferenciales parciales … Wikipedia Español

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos