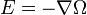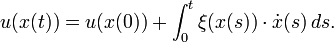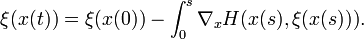Ecuación de la Eikonal

Ecuación de la Eikonal

Ecuación de la Eikonal

La Ecuación Eikonal es una Ecuación en derivadas parciales con no linealidad encontrada en propagación de ondas, cuando la ecuacion de onda es aproximada usando la Teoría WKB. Esto es derivable desde las Ecuaciones de Maxwell de electromagnetismo, y proveen un enlace entre Óptica física (onda) y Óptica geométrica (rayos).

La ecuacion Eikonal es de la forma:

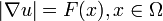
\vert \nabla u \vert = F(x), x \in \Omega

Tendiendo a 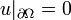u \vert_{\partial\Omega} = 0, donde Ω es un conjunto abierto dentro de 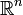\mathbb{R}^n con "Buen-comportamiento" en los limites, F(x) es una función con valores positivos, \nabla denota el gradiente y |·| es la norma Euclidiana. Aqui, el lado de la mano derecha F(x) es tipicamente suministrada como entrada conocida. 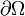Fisicamente, u(x) es el tiempo mas corto necesitado para viajar desde el limite(topologico) \partial \Omega a x dentro de Ω, con F(x) siendo el coste de tiempo (no velocidad) en x. Un algoritmo de cálculo rápido para aproximar la solución de la ecuación es la eikonal el metodo de marcha rapida. 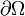En el especial caso cuando F = 1, la solución da la distancia señalada desde \partial \Omega.

Contenido

Interpretacion física

El significado fisico de la ecuacion Eikonal esta relacionada con la formula:

E = -\nabla \Omega

Donde E es la intensidad del campo electrico y Ω es el potencial eléctrico. Hay una ecuación de velocidad potencial de flujo de fluidos y la temperatura en la transferencia de calor. El significado físico de esta ecuación en el ejemplo electromagnético es que cualquier cargo que ocurren en la región es empujado hacia el exterior en un ángulo recto de las líneas de potencial y constantes viajes a lo largo de este cargo las líneas de fuerza constante dada por el ámbito del vector E. Las variables correspondientes se producen en el flujo de fluidos y la termodinámica. Ray óptica y electromagnética están relacionados por el hecho de que la ecuación eikonal da una segunda fórmula electromagnética de la misma forma que la ecuación anterior, donde el potencial de la línea de potencial constante, se ha sustituido por una línea constante de fase y la fuerza de las líneas han sido sustituidos por normales de los vectores que salen de la línea de fase constante en ángulo recto. La magnitud de estos vectores normal viene dada por la raíz cuadrada de la permitividad relativa.La línea constante de fase puede ser considerado como el borde de uno de la promoción de las ondas de luz. Los vectores son normales los rayos de la luz viaja en óptica de rayos. Esta explicación está en el sistema de RMKS unidades utilizadas por los ingenieros eléctricos.

Descripción matemática

Una ecuacion Eikonal es una de la forma

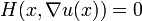
H(x,\nabla u(x)) = 0
u(0,x') = u0(x'), para x = (x1,x')

El plano x = (0,x') puede ser pensado como la primera condición, por el pensamiento de x1 como t. También se puede resolver la ecuación en un subconjunto de este avión, o en una superficie curva, con evidentes modificaciones.

Esto se muestra en la óptica geométrica, por ejemplo, cuando la ecuación es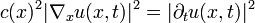c(x)^2 |\nabla_x u(x,t)|^2 = |\partial_t u(x,t)|^2. Esta es una ecuación que describe la fase de los frentes de onda. El afortunado asunto es que, en hipótesis razonables sobre el dato "inicial", la eikonal ecuación admite una solución local. Por desgracia, una solución global (por ejemplo, una solución para todos los tiempos en el caso de la óptica geométrica) no es posible. La razón es que pueden desarrollar cáusticas. En el caso de la óptica geométrica, esto significa el cruce de frentes de onda.

Podemos resolver la ecuación eikonal mediante el método de las características. Nota, sin embargo, que uno debe hacer la hipotesis "no-característica"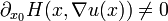\partial_{x_0} H(x,\nabla u(x)) \neq 0 for x = (0,x'). También tenemos que asumir claramente 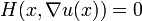H(x,\nabla u(x)) = 0, para x = (0,x').

Primero, resuelve el problema H(x,ξ(x)) = 0, 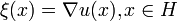\xi(x) = \nabla u(x), x\in H. Este esta hecho por definición de curvas (y valores de ξ sobre esas curvas) como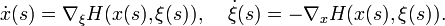

\dot x(s) = \nabla_\xi H(x(s),\xi(s)), \;\;\;\; \dot \xi(s) = -\nabla_x H(x(s),\xi(s)).
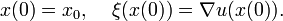x(0) = x_0, \;\;\;\; \xi(x(0)) = \nabla u(x(0)). Nota incluso que nosotros tenemos una solución u, conocemos 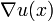\nabla u(x) para x = (0,x') debido a nuestra ecuación para H.

Estas ecuaciones tienen una solución para algún intervalo de 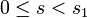0 \leq s < s_1 sigue desde teoremas estandares de EDO (Usando la hipotesis no-caracteristica). Estas curvas llenan un conjunto abierto alrededor del planox = (0,x'). Asi pues las curvas definen l valor de ξ Dentro de un conjunto abierto alrededor de nuestro plano inicial. Una vez definido como tal es facil para ver usando la regla de cadena que 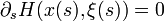\partial_s H(x(s), \xi(s)) = 0, y por tanto H = 0 a lo largo de estas curvas.

Deseamos que nuestra solucion u satisfaga 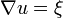\nabla u = \xi, o mas especificamente, para cada s, 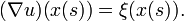(\nabla u)(x(s)) = \xi(x(s)). Asumiendo por un minuto que esto es posible, para cualquier solución u(x) debemos tener

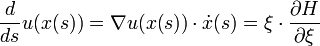\frac{d}{d s} u(x(s)) = \nabla u(x(s)) \cdot \dot x(s) = \xi \cdot \frac{\partial H}{\partial \xi},

y por tanto

u(x(t)) = u(x(0)) + \int_0^t \xi(x(s))\cdot \dot x(s)\, ds.

En otras palabras, la solución u se dará en un vecindario del plano inicial por una ecuacion explicita. Sin embargo, desde los diferentes caminos x(t), Iniciando desde diferentes puntos iniciales cruzados la solución puede llegar a ser multi-valente,al punto que hemos desarrollado cáusticas. También tenemos (incluso antes de que muestre que u es una solución)

\xi(x(t)) = \xi(x(0)) - \int_0^s \nabla_x H(x(s),\xi(x(s))).

Queda por demostrar que ξ, que hemos definido en un barrio de nuestro primer plano, es el gradiente de alguna función u. Esta seguirá si demostramos que el vector campo ξ es Rotacional Libre. Considere el primer termino en la definición de ξ. Este termino, 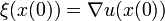\xi(x(0)) = \nabla u(x(0)) es Rotacional libre como es el gradiente de una función. En cuanto a los otros plazo, tomamos nota

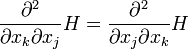\frac{\partial^2}{\partial x_k \partial x_j} H = \frac{\partial^2}{\partial x_j \partial x_k} H .

El resultado sigue

Véase también

Referencias

  • Paris, D. T. and Hurd F.K., Basic Electromagnetic Theory, McGraw-Hill 1969, pg. 383-385.
  • Arnold, V. I., Lectures on Partial Differential Equations, Springer 2004, 2nd Edition, pg. 2-3.

Enlaces externos

Obtenido de "Ecuaci%C3%B3n de la Eikonal"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Ecuación de Schrödinger — Saltar a navegación, búsqueda La ecuación de Schrödinger fue desarrollada por el físico austríaco Erwin Schrödinger en 1925. Describe la evolución temporal de una partícula masiva no relativista. Es de importancia central en la teoría de la… …   Wikipedia Español

  • Función distancia con signo — En matemáticas la función distancia con signo mide cuan cerca se encuentra un punto x de un conjunto S otrogándole un signo según el punto se encuentre de un lado o de otro del conjunto S. donde es la distancia ordinaria de un punto a un conjunto …   Wikipedia Español

  • Aproximación WKB — En Física, la aproximación WKB es el ejemplo más familiar de un cálculo semi clásico (ver antigua teoría cuántica) en el cual la función de onda es redactada como una función exponencial, semiclásicamente expandida, y entonces o la amplitud o la… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”