La esbeltez mecánica, también denominada esbeltez, es una característica mecánica de las barras estructurales o prismas mecánicos que relaciona la rigidez de la sección transversal de una pieza prismática con su longitud total. Se caracteriza por un parámetro adimensional que interviene en el cálculo de las tensiones y predice las inestabilidades elásticas de las barras.

Además se distingue entre los valores de esbeltez natural dependientes sólo de las propiedades geométricas y mecánicas de la barra y esbeltez efectiva que contabiliza también las condiciones de enlace o sujeción en los extremos de la barra.

Contenido 1 Esbeltez flexional 1.1 Esbeltez flexional relativa (eurocódigo) 2 Esbeltez torsional 2.1 Esbeltez torsional relativa (eurocódigo)

Esbeltez flexional

Si sobre una barra esbelta recta se aplica un esfuerzo normal de compresión, además de acortamiento de la misma aparece una deflexión desde la forma recta, lo que se conoce como pandeo, la magnitud de cuyo efecto depende de la llamada esbeltez mecánica flexional, o simplemente esbeltez mecánica efectiva, que viene dada por:

(1)

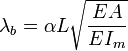
Donde:

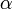, es un valor adimensional que relaciona la esbeltez flexional natural y la esbeltez flexional, depende de las condiciones de enlace en los extremos (ver más abajo).

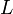, es la longitud real de la barra.

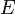, es el módulo de Young.

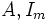, son respectivamente el valor del área de la sección transversal y del segundo momento de área o momento de inercia mínimo de la sección transversal.

La fórmula (1) también puede escribirse como:

(2)

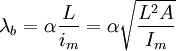
Donde L es la longitud natural de la barra, i_m el "radio de giro" mínimo (el menor de los dos posibles), A el área de la sección de la barra, I_m el menor momento de área y α un coeficiente que dependiente del tipo de sujeción de los extremos de la barra, por ejemplo:

• α = 2.00 Empotrada-Libre
• α = 1.00 Biarticulada
• α = 0.71 Empotrada-Articulada
• α = 0.50 Biempotrada

En ocasiones el producto αL es denominado longitud de pandeo (L_p). Si se prescinde del valor de α en las fórmulas (1) y (2) se obtiene la esbeltez flexional natural de la barra.

Esbeltez flexional relativa (eurocódigo)

Algunas normas como la norma europea eurocódigo 3 usan la llamada esbeltez relativa donde que se obtiene de comparar la esbeltez flexional convencional un factor adimiensional que depende de las características de la sección y el material dicha esbeltez relativa viene dada por:

(3)

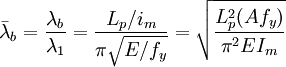
Donde:

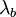, esbeltez flexional convencional.

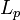, longitud de pandeo.

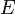, es el módulo de Young.

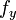, es la tensión de límite elástico del material.

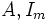, son respectivamente el valor del área de la sección transversal y del segundo momento de área o momento de inercia mínimo de la sección transversal.

Esbeltez torsional

La esbeltez mecánica torsional, o simplemente esbeltez torsional, es un parámetro adimensional que mide el grado de alabeo que presentará una sección al ser sometida a esfuerzos de torsión que viene dado por:

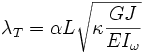
Donde:

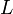, es la longitud natural de la barra.

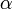, es un valor adimensional que relaciona la esbeltez torsional natural y la esbeltez torsional efectiva y toma los mismos valores para la esbeltez flexional según sean las condiciones de enlace en los extremos.

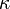, es un parámetro relacionado con el esfuerzo cortante, que para barras esbeltas es cercano a 1.

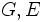, son respectivamente el módulo de elasticidad transversal y el módulo de elasticidad longitudinal.

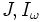, son respectivamente el módulo de torsión y el módulo de alabeo.

Esbeltez torsional relativa (eurocódigo)