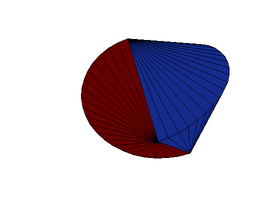
- Esfericón
-
Esfericón
El esfericón es un cuerpo geométrico que posee una única cara, dos aristas y cuatro vértices. Fue descubierto por el inglés Colin Roberts en 1969. En 1999 su descubrimiento llamó la atención de Ian Stewart que más tarde publicó un artículo sobre el mismo en la revista Scientific American.[1]
Para construir un esfericón basta con tomar un bicono con ápices de 90 grados de apertura y cortarlo a lo largo del plano que une ambos ápices. Luego se debe rotar 90 grados una de las mitades y pegar nuevamente ambas partes.
La curva suave de la costura de una pelota de tenis queda determinada por el contacto de una esfera inscrita a un esfericón.[2]
Contenido
Características[3]
Una característica del esfericón es que rueda sobre una superficie plana. Al contrario de un cono que rueda describiendo círculos, el esfericón realiza un movimiento con balanceos, que en promedio es recto. En un principio uno de los sectores cónicos entra en contacto con la superficie plana y luego el otro. Es por eso que a medida que progresa su movimiento se bambolea alternativamente de derecha a izquierda.
El esfericón posee una única superficie continua, lo que permite hacer rodar dos esfericones uno sobre otro indefinidamente. Cuatro esfericones ubicados en un bloque cúbico pueden rodar unos sobre otros de manera simultánea. También es posible hacer rodar cuatro esfericones de manera simultánea sobre la superficie de un quinto esfericón. Y ocho esfericones se pueden situar en la superficie de un esfericón de manera tal que cualquiera de los sólidos exteriores pueda rodar sobre la superficie del esfericón central.
La razón por la que el esfericón posee dichas propiedades geométricas es que la intersección de sus distintas líneas conforman un octaedro regular. El octaedro regular se relaciona de una manera particular con el cubo ya que es su poliedro dual: si se marca un punto en el punto medio de cada cara de un cubo y se une dichos puntos mediante segmentos se obtiene un octaedro regular. Y los cubos se caracterizan por la manera regular en que se pueden apilar para formar una capa plana o llenar un espacio tridimensional.
Familia de los esfericones
El esfericón se construye a partir de un bicono cuyo corte con un plano pasante por su eje de simetría es un cuadrado. Es posible construir diferentes sólidos pertenecientes a la familia del esfericón y clasificarlos en función del tipo de corte que posee la figura de revolución a partir de la cual se los genera. La manera de construirlos es la siguiente:[4]
- Se divide un polígono regular de n lados por la mitad. Dependiendo del polígono el corte puede pasar por dos vértices (V-V), por un vértice y el punto medio de un lado (V-L) o por el punto medio de dos lados (L-L).
- A partir de la mitad obtenida se construye un sólido de revolución haciendo girar dicha mitad alrededor del eje a lo largo del cual se realizó el corte.
- Se divide el sólido de revolución por la mitad mediante un corte que pasa por el eje de simetría.
- Se rota una de las mitades en sentido horario en 360 / i grados, con i = n,n − 1,...,1
En la siguiente tabla se detalla la secuencia de construcción de algunos cuerpos de la familia del esfericón, generados a partir de un polígono de n lados:[5] [6]
Lados del polígono Eje de revolución Sólido de revolución Giro [grados] Caras Caras continuas Aristas Aristas continuas Cuerpo terminado 3 
Cono con ápice de 60 grados 120 1 0 1 0 Semiesfericón 4 
Bicono con ápices de 90 grados 90 1 1 2 0 Esfericón 
Cilindro 90 2 0 1 1 5 
72 1 0 1 0 144 1 0 1 0 6 
"Lápiz de dos puntas" 60 1 1 2 0 Hexaesfericón 
60 2 0 1 1 7 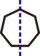
51 1 0 1 0 103 1 0 1 0 154 1 0 1 0 8 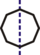
45 1 1 2 0 Octaesfericón 90 2 2 3 1 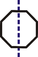
"Lápiz de dos puntas planas" 45 2 0 1 1 90 3 1 2 2 Esfericón truncado Los sólidos cuyo corte tiene un número impar de lados son diferentes a los que poseen un número par de lados. Poseen un único camino en su superficie, pero el mismo se ve truncado en los extremos: no es continuo como en el caso de los sólidos cuyo corte tiene un número par de lados y cuyo eje de rotación es vértice-vértice.
Véase también
Referencias
- ↑ Mathematical Recreations - Cone with a Twist, Scientific American, vol. 281, no. 4, Oct. 1999, pp. 116-117
- ↑ Costura de una pelota de tenis (francés)
- ↑ National curve bank
- ↑ How Sphericons are connected
- ↑ Sphericon Series
- ↑ The N-icon Study
Enlaces externos
- The Sphericon Homepage (inglés)
- Construcción de esfericones de diferentes materiales
- Epsilones: Construcción y otras referencias.
- Modelos de esfericón en papel
- The Sphericon
- Visualización interactiva del esfericón (requiere del Wolfram Mathematica Player)
- Weisstein, Eric W. "Sphericon." From MathWorld--A Wolfram Web Resource.
Categoría: Figuras geométricas
Wikimedia foundation. 2010.