Cono (geometría)

Cono (geometría)
Para otros usos de este término, véase cono.
Cone.jpg

En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al punto donde confluyen las generatrices se llama vértice.

Superficie cónica se denomina a toda superficie reglada conformada por el conjunto de rectas que teniendo un punto común (el vértice), intersecan a una circunferencia no coplanaria.

Contenido

Clasificación

Cono recto y cono oblicuo.

Se denominan:

  • Cono recto, si el vértice equidista de la base circular
  • Cono oblicuo, si el vértice no equidista de su base
  • Cono elíptico, si la base es una elipse. Pueden ser rectos u oblicuos.

La generatriz de un cono es cada uno de los segmentos cuyos extremos son el vértice y un punto de la circunferencia de la base.

La altura de un cono es la distancia del vértice al plano de la base. En los conos rectos será la distancia del vértice al centro de la circunferencia de la base.

Área de la superficie cónica

El área A\, de la superficie del cono recto es:

A=A_{Base}+ A_{Lateral}=\pi r^2 + \pi rg\,\!

donde r es el radio de la base y g la longitud de la generatriz del cono recto.

La generatriz de un cono recto equivale a la hipotenusa del triángulo rectángulo que conforma con la altura del cono y el radio de la base;

su longitud es: g=\sqrt{h^2+r^2}\,.

Desarrollo plano de un cono recto

Desarrollo plano del cono.

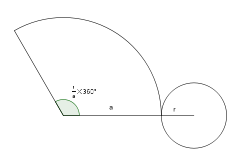
El desarrollo plano de un cono recto es un sector circular y un círculo.

El sector circular está delimitado por dos generatrices, siendo la medida del lado curvo igual a la longitud de la circunferencia de la base.

La forma de calcular la distancia a en el desarrollo es con la ecuación de a=\sqrt{h^2+r^2}\,

donde r es el radio de la base y h es la altura del cono.

El ángulo que esta sombreado en la figura se calcula con la siguiente fórmula:

\mathrm{\acute{a}ngulo} = 360(r/a) \,.

Volumen de un cono

El volumen V\, de un cono de radio r \, y altura h \, es 1/3 del volumen del cilindro que posee las mismas dimensiones:

V = \frac{\pi \cdot r^2 \cdot h}{3}\,\!

La ecuación se obtiene mediante \int^{h}_{0}A(x)dx\,\!,

donde A(x)\, es el área de la sección perpendicular a la altura, con relación a la altura h, en este caso A(x)=\pi\left(\frac{rx}{h}\right)^2.

Secciones cónicas

Distintas secciones cónicas.
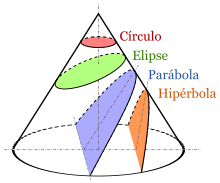
Artículo principal: Sección cónica

Al cortar con un plano a una superficie cónica, se obtiene distintas figuras geométricas: las secciones cónicas. Dependiendo del ángulo de inclinación y la posición relativa, pueden ser: circunferencias, elipses, parábolas e hipérbolas.

Si el plano pasa por el vértice la intersección podrá ser: una recta, un par de rectas cruzadas o un punto (el vértice).

Las curvas cónicas son importantes en astronomía: dos cuerpos masivos que interactúan según la ley universal de la gravitación, describen órbitas similares a secciones cónicas: elipses, hipérbolas o parábolas en función de sus distancias, velocidades y masas.

También son muy útiles en aerodinámica y otras aplicaciones industriales, ya que permiten ser reproducidas por medios simples con gran exactitud, logrando volúmenes, superficies y curvas de gran precisión.

Ecuación en coordenadas cartesianas

Superficie cónica.

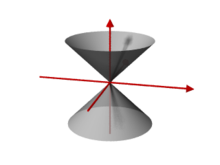
En Geometría analítica y Geometría diferencial, el cono es el conjunto de puntos del espacio que verifican, respecto un sistema de coordenadas cartesianas, una ecuación del tipo:

\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} = 0 \,

Este conjunto también coincide con la imagen de la función:

X(\theta,t)=(a \cdot t \cdot \cos(\theta),b \cdot t \cdot \sin(\theta),c \cdot t),\,

que es llamada parametrización del cono.

Por ejemplo, en el caso que a = b (no nulos), éste conjunto es obtenido a partir de rotar la recta (t,0,\frac{c\,t}{a})\, respecto al eje z, y por eso es llamada parametrización de revolución.

El cono no es una superficie regular, pues posee una singularidad: su vértice; quitándolo se convierte en una superficie regular disconexa y abierta. Entre sus características, podemos destacar que es una superficie reglada (es decir que se puede generar por el movimiento de una recta), y es desarrollable, es decir, que se puede desplegar sobre un plano; técnicamente esto se expresa diciendo que su curvatura gaussiana es nula (como en el plano o el cilindro)

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Cono (geometría) — Un cono es un sólido geométrico formado por la revolución de un triángulo rectángulo alrededor de uno de sus catetos. El cono se representa en un sistema de coordenadas cartesianas mediante la ecuación: El volumen del cono es , donde r es el… …   Enciclopedia Universal

  • Geometría del espacio — La geometría del espacio es rama de la geometría que se ocupa de las propiedades y medidas de figuras geométricas en el espacio tridimensional. Entre estas figuras, también llamadas sólidos, se encuentran el cono, el cubo, el cilindro, la… …   Enciclopedia Universal

  • cono — sustantivo masculino 1. Área: geometría Cuerpo geométrico limitado por una base circular y una superficie formada por rectas que parten de esta circunferencia y convergen en un mismo punto. 2. Objeto que tiene esta forma: un sombrero de papel con …   Diccionario Salamanca de la Lengua Española

  • Cono — (Del lat. conus < gr. konos, cono, piña.) ► sustantivo masculino 1 GEOMETRÍA Cuerpo geométrico limitado por una superficie cónica, cuya directriz es una circunferencia, y por un plano, que forma su base, y que la corta. 2 GEOMETRÍA Superficie… …   Enciclopedia Universal

  • Geometría analítica — La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la… …   Wikipedia Español

  • Geometría — (Del gr. geometria, agrimensura, geometría.) ► sustantivo femenino 1 GEOMETRÍA, MATEMÁTICAS Parte de las matemáticas que estudia el espacio y las figuras y cuerpos que en él se pueden imaginar. FRASEOLOGÍA geometría analítica GEOMETRÍA,… …   Enciclopedia Universal

  • Geometría descriptiva — La geometría descriptiva es un conjunto de técnicas de carácter geométrico que permite representar el espacio tridimensional sobre una superficie bidimensional y, por tanto, resolver en dos dimensiones los problemas espaciales garantizando la… …   Wikipedia Español

  • Cono — El término cono puede referirse a: geometría: cono, figura geométrica de revolución. biología: cono, célula fotorreceptora de la retina que recibe las impresiones luminosas del color, cono, un molusco gasterópodo, cono o estróbilo, estructura de… …   Wikipedia Español

  • Geometría espacial — Se ha sugerido que este artículo o sección sea fusionado en Geometría de los cuerpos sólidos (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí …   Wikipedia Español

  • geometría — Estudio matemático del espacio y de los elementos que lo componen, por ejemplo puntos, líneas, planos y volúmenes: * La Geometría plana trata de los puntos, las líneas y los planos de dos dimensiones; * La Geometría del espacio, de los cuerpos… …   Diccionario ecologico

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”