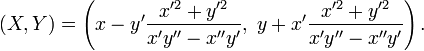Evoluta

Evoluta

Evoluta

Se llama evoluta de una curva "C" dada, al lugar geométrico de los centros de curvatura de "C".

Contenido

Ecuaciones

Sea la curva formada por el conjunto de puntos (x,y) donde x e y son funciones dependientes de una variable, normalmente llamada t para hacer referencia al tiempo. Entonces se puede escribir las coordenadas de la evoluta de la forma

(X, Y)= \left({x-y'\frac{x'^2+y'^2}{x'y''-x''y'},\; y+x'\frac{x'^2+y'^2}{x'y''-x''y'}}\right).

donde a cada (x,y) - o lo que es lo mismo, a un valor de t que determina un punto de la curva - le corresponde un centro de curvatura (X,Y) en función de ese t. La relación entre ese punto y su centro de curvatura permite conocer el radio de curvatura (y por tanto su inversa, la curvatura):
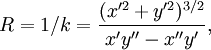
R = 1/k = \frac{(x'^2+y'^2)^{3/2}}{x'y''-x''y'},

Si y=f(x), es decir, una variable depende de la otra, se puede simplificar observando los resultados de tomar x=t e y=f(t). Los centros de curvatura serán entonces:
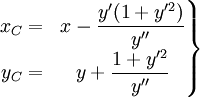\left . \begin{matrix} x_C = & x- \displaystyle \frac {y'(1+y'^2)}{y''} \\ y_C = & y+ \displaystyle\frac {1+y'^2}{y''} \end{matrix} \right \} y el radio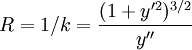 R = 1/k = \frac{(1+y'^2)^{3/2}}{y''}

Eliminando x e y entre ellas se tiene la ecuación de la evoluta:

F(xC,yC) = 0

Ejemplos de evolutas

Evoluta de la elipse con a=1 y b=2

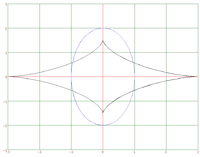
Evoluta de la elipse

Dada la elipse:

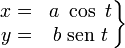
\left . \begin{matrix} x = & a\ \cos\ t \\ y = & b\ \mathrm{sen}\ t \end{matrix} \right \}

Su evoluta viene dada por:

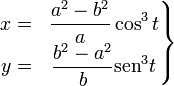\left . \begin{matrix} x = & \displaystyle\frac {a^2 - b^2}{a} \cos ^3 t \\ y = & \displaystyle\frac {b^2 - a^2}{b} \mathrm{sen}^3 t \end{matrix} \right \} que, eliminando el parámetro, queda: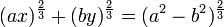 (ax)^\frac{2}{3} + (by)^\frac{2}{3} = (a^2 - b^2)^\frac{2}{3}

Enlaces externos

La evoluta en MathWorld (en inglés)

Obtenido de "Evoluta"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • evolută — EVOLÚTĂ, evolute, s.f. (mat.) Curbă, loc geometric al centrelor de curbură ale unei curbe date; desfăşurată. – Din germ. Evolute. Trimis de ionel bufu, 14.06.2004. Sursa: DEX 98  EVOLÚTĂ s. v. desfăşurată. Trimis de siveco, 13.09.2007. Sursa:… …   Dicționar Român

  • evoluta — evolúta ž DEFINICIJA mat. ravninska krivulja koja spaja središta zakrivljenosti neke druge ravninske krivulje (njezine evolvente) ETIMOLOGIJA lat. (linea) evoluta ≃ evolutus ← evolvere: odmotati, razviti …   Hrvatski jezični portal

  • Evoluta —         (лат.) выявленное, открытое. Философский энциклопедический словарь. М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983 …   Философская энциклопедия

  • evolúta — ž mat. ravninska krivulja koja spaja središta zakrivljenosti neke druge ravninske krivulje (njezine evolvente) ✧ {{001f}}lat …   Veliki rječnik hrvatskoga jezika

  • evoluta — s. f. [Geometria] Curva em que estão os centros de outra curva evolvente …   Dicionário da Língua Portuguesa

  • evoluta — f Lugar de los centros de curvatura de una curva plana o la envolvente de sus normales …   Diccionario de Construcción y Arquitectur

  • evoluta — e|vo|lu|ta Mot Pla Nom femení …   Diccionari Català-Català

  • evoluta — e·vo·lù·ta s.f. TS geom. curva luogo geometrico dei centri di curvatura di un evolvente {{line}} {{/line}} DATA: 1875. ETIMO: der. di evoluto …   Dizionario italiano

  • evoluta — pl.f. evolute …   Dizionario dei sinonimi e contrari

  • evoluta —   , evolutum   L. evolvo, unroll. Leaf blades short …   Etymological dictionary of grasses

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”