Extrapolación de Richardson

Extrapolación de Richardson: Extrapolación de Richardson

Saltar a navegación, búsqueda

El método de extrapolación de Richardson fue desarrollado por Lewis Fry Richardson (1881-1953). Se puede utilizar para mejorar los resultados de un método numérico a partir de una estimación de igual forma mejora la precisión en el cálculo numérico de la derivada de una función, partiendo de la base de la serie de Taylor. Este proceso es especialmente utilizado para definir un método de integración: El método de Romberg.

Presentación del principio

Para una función variable en x, la primera derivada está definida por:

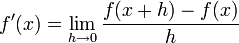
$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Una simple aproximación se tiene por la diferencia hacia adelante, de forma que: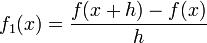

$f_{1}(x)=\frac{f(x+h)-f(x)}{h}$

Ésta aproximación está lejos del valor real, por tanto en órden de hacer un análisis del error, expandimos en forma de serie de Taylor: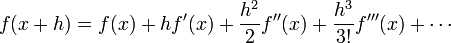 $f(x+h)=f(x)+hf'(x)+\frac{h^2}{2}f''(x)+\frac{h^3}{3!}f'''(x)+ \cdots$

Subtrayendo f(x) de ambos lados y dividiendo por h, se tiene que: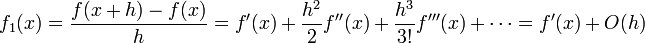

$f_{1}(x)=\frac{f(x+h)-f(x)}{h}= f'(x)+\frac{h^2}{2}f''(x)+\frac{h^3}{3!}f'''(x)+ \cdots= f'(x) + O(h)$

Analogamente se derivan las demás fórmulas de aproximación, deduciendo por ejemplo, con diferencia hacia atrás o cambiando los valores de h; de está forma se obtiene una expresión generalizada llamada extrapolación de richardson, de la siguiente forma:

Sea A, la respuesta exacta a la integral, y A(h) la estimación de A con órden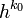 $h^{k_0}$ . De tal forma que: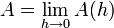

$A = \lim_{h \to 0} A(h)$

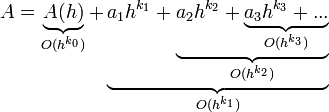
$A = \underbrace{A(h)}_{O(h^{k_0})} + \underbrace{a_{1}h^{k_1}+ \underbrace{a_{2}h^{k_2} + \underbrace{a_{3}h^{k_3}+ ...}_{O(h^{k_3})}}_{O(h^{k_2})}}_{O(h^{k_1})}$

Donde:

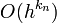$O(h^{k_n})$ es un estimador del error, usando la notación de Landau.

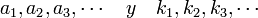$a_{1}, a_{2}, a_{3},\cdots y k_{1}, k_{2}, k_{3},\cdots$ son constantes desconocidas. Tal que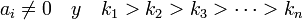 $a_{i}\neq 0 y k_{1} > k_{2} > k_{3}> \cdots > k_{n}$

Ahora bien: Usando tamaños de espaciamiento h y h/t, podemos aproximar a A como: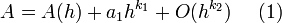

$A = A(h) + a_{1}h^{k_1}+ O(h^{k_2})~(1)$

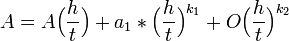
$A = A\Big(\frac{h}{t}\Big) + a_{1}*\Big(\frac{h}{t}\Big)^{k_1}+ O\Big(\frac{h}{t}\Big)^{k_2}$

Multiplicando la última ecuación por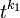 $t^{k_1}$

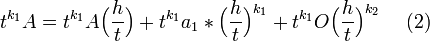
$t^{k_1}A = t^{k_1}A\Big(\frac{h}{t}\Big) + t^{k_1}a_{1}*\Big(\frac{h}{t}\Big)^{k_1}+ t^{k_1}O\Big(\frac{h}{t}\Big)^{k_2}~(2)$

Sustrayendo (2) y (1), como se vio al inicio:

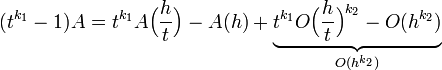
$(t^{k_1}-1)A = t^{k_1}A\Big(\frac{h}{t}\Big) - A(h) + \underbrace{t^{k_1}O\Big(\frac{h}{t}\Big)^{k_2} - O(h^{k_2})}_{O(h^{k_2})}$

Despejando A:

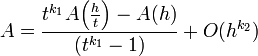
$A = \frac{t^{k_1}A\Big(\frac{h}{t}\Big) - A(h)}{(t^{k_1}-1)} + O(h^{k_2})$

De este modo, se ha obtenido una mejor aproximación de A al sustraer el término más grande en el error, 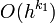$O(h^{k_1})$ . De igual manera se pueden remover más términos de error de modo que se obtengan mejores aproximaciones de A. Una relación de recurrencia general puede ser implementada en las aproximaciones al hacer:

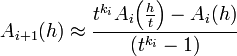$A_{i+1}(h)\approx \frac{t^{k_i}A_{i}\Big(\frac{h}{t}\Big) - A_{i}(h)}{(t^{k_i}-1)}$ siendo $k i$ el órden del error.

con

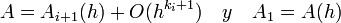$A = A_{i+1}(h) + O(h^{k_{i}+1})y A_{1} = A(h)$

Obtenido de "Extrapolaci%C3%B3n de Richardson"

Categorías: Análisis numérico | Análisis asintótico

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Lewis Fry Richardson — D.Sc., Miembro de la Royal Society Nacimiento 11 de octubre de 1881 Newcastle upon Tyne … Wikipedia Español
Integración numérica — En análisis numérico, la integración numérica constituye una amplia gama de algoritmos para calcular el valor numérico de una integral definida y, por extensión, el término se usa a veces para describir algoritmos numéricos para resolver… … Wikipedia Español
Método de Romberg — En análisis numérico, el Método de Romberg genera una matriz triangular cuyos elementos son estimaciones numéricas de la integral definida siguiente: usando la extrapolación de Richardson de forma reiterada en la regla del trapecio. El método de… … Wikipedia Español
Takebe Kenkō — Takebe Katahiro (Japonés:建部賢弘); * 1664; † 1739) o Takebe Kenkō fue un matemático japonés de la corriente del wasan. Fue estudiante de Seki Takakazu y jugó un rol crítico en el desarrollo del Enri (Japonés: 円理, principio del círculo ) – un… … Wikipedia Español
Interpolación polinómica — En análisis numérico, la interpolación polinómica es una técnica de interpolación de un conjunto de datos o de una función por un polinomio. Es decir, dado cierto número de puntos obtenidos por muestreo o a partir de un experimento se pretende… … Wikipedia Español
Computación Científica — La Computación Científica (o Ciencia Computacional) es el campo de estudio relacionado con la construcción de modelos matemáticos y técnicas numéricas para resolver problemas científicos, de ciencias sociales y problemas de ingeniería.… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Extrapolación de Richardson

Extrapolación de Richardson

Presentación del principio

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Extrapolación de Richardson

Extrapolación de Richardson

Presentación del principio

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo