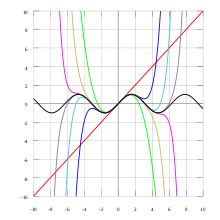
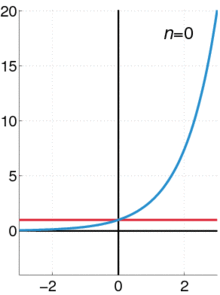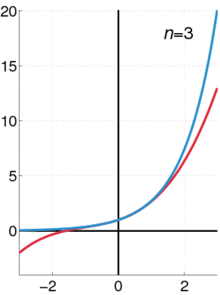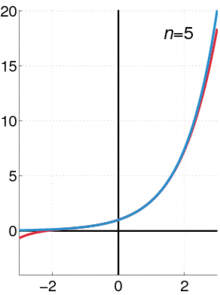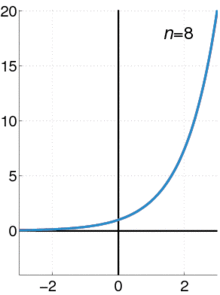
Serie de Taylor

Serie de Taylor
sin(x) y aproximaciones de Taylor centradas en 0, con polinomios de grado 1, 3, 5, 7, 9, 11 y 13.

En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define como la siguiente suma:

La función exponencial (en azul), y la suma de los primeros n+1 términos de su serie de Taylor en torno a cero (en rojo).

f(x) = \sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}

Aquí, n! es el factorial de n y f (n)(a) indica la n-ésima derivada de f en el punto a.

Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.

Si a = 0, a la serie se le llama serie de Maclaurin.

Esta representación tiene tres ventajas importantes:

  • La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
  • Se puede utilizar para calcular valores aproximados de la función.
  • Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.

Algunas funciones no se pueden escribir como serie de Taylor porque tienen alguna singularidad. En estos casos normalmente se puede conseguir un desarrollo en serie utilizando potencias negativas de x (véase Serie de Laurent. Por ejemplo f(x) = exp(−1/x²) se puede desarrollar como serie de Laurent.

Contenido

Definición

La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:

f(x) = f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots

que puede ser escrito de una manera más compacta como

f(x) = \sum_{n=0}^{\infin} \frac{f^{(n)}(a)}{n!} (x-a)^{n}\,,

donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.

Historia

El filósofo eleata Zenón de Elea consideró el problema de sumar una serie infinita para lograr un resultado finito, pero lo descartó por considerarlo imposible: el resultado fueron las paradojas de Zenón. Posteriormente, Aristóteles propuso una resolución filosófica a la paradoja, pero el contenido matemático de esta no quedó resuelto hasta que lo retomaron Demócrito y después Arquímedes. Fue a través del método exhaustivo de Arquímedes que un número infinito de subdivisiones geométricas progresivas podían alcanzar un resultado trigonométrico finito.[1] Independientemente, Liu Hui utilizó un método similar cientos de años después.[2]

En el siglo XIV, los primeros ejemplos del uso de series de Taylor y métodos similares fueron dados por Madhava de Sangamagrama.[3] A pesar de que hoy en día ningún registro de su trabajo ha sobrevivido a los años, escritos de matemáticos hindúes posteriores sugieren que él encontró un número de casos especiales de la serie de Taylor, incluidos aquellos para las funciones trigonométricas del seno, coseno, tangente y arcotangente.

En el siglo XVII, James Gregory también trabajó en esta área y publicó varias series de Maclaurin. Pero recién en 1715 se presentó una forma general para construir estas series para todas las funciones para las que existe y fue presentado por Brook Taylor, de quién recibe su nombre.

Las series de Maclaurin fueron nombradas así por Colin Maclaurin, un profesor de Edinburgo, quién publicó el caso especial de las series de Taylor en el siglo XVIII.

Series de Maclaurin (Taylor alrededor de 0) notables

La función coseno.
Una aproximación de octavo orden de la función coseno en el plano de los complejos.
Las dos imágenes de arriba puestas juntas.

A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos de x.

Función exponencial y logaritmo natural

e^{x} = \sum^{\infin}_{n=0} \frac{x^n}{n!}\quad, \forall x; n \in \mathbb{N}_0
\ln(1+x) = \sum^{\infin}_{n=1} \frac{(-1)^{n+1}}n x^n\quad\mbox{, para } \left| x \right| < 1

Serie geométrica

\frac{1}{1-x} = \sum^{\infin}_{n=0} x^n\quad\mbox{ para } \left| x \right| < 1

Teorema del binomio

(1+x)^\alpha = \sum^{\infin}_{n=0} \frac{\Gamma(\alpha+1)}{\Gamma(n+1)\Gamma(n-\alpha)} x^n\quad para \left| x \right| < 1\quad

y cualquier \alpha\quad complejo

Funciones trigonométricas

\sin x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\quad, \forall x
\cos x = \sum^{\infin}_{n=0} \frac{(-1)^n}{(2n)!} x^{2n}\quad, \forall x
\tan x = \sum^{\infin}_{n=1} \frac{B_{2n} (-4)^n (1-4^n)}{(2n)!} x^{2n-1}\quad, \mbox{ para } \left| x \right| < \frac{\pi}{2}
Donde Bs son los Números de Bernoulli.
\sec x = \sum^{\infin}_{n=0} \frac{(-1)^n E_{2n}}{(2n)!} x^{2n}\quad\mbox{, para } \left| x \right| < \frac{\pi}{2}
\csc{x}=\sum_{n=1}^\infty{\frac{2(2^{2n-1}-1)B_{n}x^{2n-1}}{(2n)!}}\quad\mbox{, para } 0<\left |{x}\right |< \pi
\arcsin x = \sum^{\infin}_{n=0} \frac{(2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
\arctan x = \sum^{\infin}_{n=0} \frac{(-1)^n}{2n+1} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1

Funciones hiperbólicas

\sinh x = \sum^{\infin}_{n=0} \frac{1}{(2n+1)!} x^{2n+1}\quad , \forall x
\cosh x = \sum^{\infin}_{n=0} \frac{1}{(2n)!} x^{2n}\quad , \forall x
\tanh x = \sum^{\infin}_{n=1} \frac{B_{2n} 4^n (4^n-1)}{(2n)!} x^{2n-1}\quad\mbox{, para } \left| x \right| < \frac{\pi}{2}
\sinh^{-1} x = \sum^{\infin}_{n=0} \frac{(-1)^n (2n)!}{4^n (n!)^2 (2n+1)} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1
\tanh^{-1} x = \sum^{\infin}_{n=0} \frac{1}{2n+1} x^{2n+1}\quad\mbox{, para } \left| x \right| < 1

Función W de Lambert

W_0(x) = \sum^{\infin}_{n=1} \frac{(-n)^{n-1}}{n!} x^n\quad\mbox{, para } \left| x \right| < \frac{1}{e}

Los números Bk que aparecen en los desarrollos de tan(x) y tanh(x) son Números de Bernoulli. Los valores C(α,n) del desarrollo del binomio son los coeficientes binomiales. Los Ek del desarrollo de sec(x) son Números de Euler.

Varias variables

La serie de Taylor se puede generalizar a funciones de d variables:

\sum_{n_1=0}^{\infin} \cdots \sum_{n_d=0}^{\infin} \frac{\partial^{n_1}}{\partial x_1^{n_1}} \cdots \frac{\partial^{n_d}}{\partial x_d^{n_d}} \frac{f(a_1,\cdots,a_d)}{n_1!\cdots n_d!} (x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d} =
\sum_{n=0}^{\infty} {1 \over n!} \sum_{n_1+\cdots+n_d=n} {n \choose n_1 \cdots n_d} {\partial^n f(a_1,\cdots,a_d) \over \partial x_1^{n_1} \cdots \partial x_d^{n_d}} (x_1-a_1)^{n_1}\cdots (x_d-a_d)^{n_d},

donde {n \choose n_1 \cdots n_d} es un coeficiente multinomial. Como ejemplo, para una función de 2 variables, x e y, la serie de Taylor de segundo orden en un entorno del punto (a, b) es:

f(x,y) \,
\approx f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b) \,
+ \frac{1}{2}\left( f_{xx}(a,b)(x-a)^2 + 2f_{xy}(a,b)(x-a)(y-b) + f_{yy}(a,b)(y-b)^2 \right).

Un polinomio de Taylor de segundo grado puede ser escrito de manera compacta así:

T(\mathbf{x}) = f(\mathbf{a}) + \nabla f(\mathbf{a})^T (\mathbf{x} - \mathbf{a}) + \frac{1}{2} (\mathbf{x} - \mathbf{a})^T \nabla^2 f(\mathbf{a}) (\mathbf{x} - \mathbf{a}) + \cdots

donde \nabla f(\mathbf{a}) es el gradiente y \nabla^2 f(\mathbf{a}) es la matriz hessiana. Otra forma:

T(\mathbf{x}) = \sum_{|\alpha| \ge 0}^{}{\frac{\mathrm{D}^{\alpha}f(\mathbf{a})}{\alpha !}(\mathbf{x}-\mathbf{a})^{\alpha}}

Aplicaciones

Además de la obvia aplicación de utilizar funciones polinómicas en lugar de funciones de mayor complejidad para analizar el comportamiento local de una función, las series de Taylor tienen muchas otras aplicaciones.

Algunas de ellas son: análisis de límites y estudios paramétricos de los mismos, estimación de números irracionales acotando su error, teorema de L'Hopital para la resolución de límites indeterminados, estudio de puntos estacionarios en funciones (máximos o mínimos relativos o puntos sillas de tendencia estrictamente creciente o decreciente), estimación de integrales, determinación de convergencia y suma de algunas series importantes, estudio de orden y parámetro principal de infinitésimos, etc.

Véase también

Referencias

  1. ↑ Kline, M. (1990) Mathematical Thought from Ancient to Modern Times. Oxford University Press. pp. 35-37.
  2. ↑ Boyer, C. and Merzbach, U. (1991) A History of Mathematics. John Wiley and Sons. pp. 202-203.
  3. ↑ «Neither Newton nor Leibniz - The Pre-History of Calculus and Celestial Mechanics in Medieval Kerala». MAT 314. Canisius College.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Serie de Taylor — Série de Taylor Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Série de taylor — Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Série de Taylor — Pour les articles homonymes, voir Taylor. En mathématiques, et plus précisément en analyse, la série de Taylor d une fonction f (au voisinage d un point a) est une série entière construite à partir de f et de ses dérivées successives en a …   Wikipédia en Français

  • Serie de Taylor — En matemáticas, la serie de Taylor de formula función f infinitamente derivable (real o compleja) definida en un intervalo abierto (a r, a+r) se define con la siguiente suma: Aquí …   Enciclopedia Universal

  • série de Taylor — Teiloro eilutė statusas T sritis fizika atitikmenys: angl. Taylor series vok. Taylorsche Reihe, f rus. ряд Тэйлора, m pranc. série de Taylor, f; série taylorienne, f …   Fizikos terminų žodynas

  • Développement en série de Taylor — Série de Taylor Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Série de MacLaurin — Série de Taylor Pour les articles homonymes, voir Taylor. Brook Taylor, Celui dont la série porte le nom. En analyse, la série de Taylor …   Wikipédia en Français

  • Série numérique — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Série semi-convergente — Série (mathématiques) Pour les articles homonymes, voir Série. En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L étude des séries consiste à effectuer la somme d un nombre fini …   Wikipédia en Français

  • Serie entiere — Série entière Pour les articles homonymes, voir Entier (homonymie). En mathématiques et particulièrement en analyse, une série entière est une série de fonctions de la forme où les coefficients an forment une suite réelle ou complexe. La série… …   Wikipédia en Français

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”