Filtro de Chebyshov

Filtro de Chebyshov

Filtro de Chebyshov

Los filtros de Chebyshov (a veces erróneamente transcritos como Chebyshev) son un tipo de filtro electrónico, puede ser tanto analógico como digital.

Contenido

Historia

Nombrados en honor de Pafnuti Chebyshev, están relacionados con los filtros de Butterworth. Este nombre se debe a que sus características matemáticas se derivan del uso de los polinomios de Chebyshev.

Descripción

En los filtros de Chebyshev lo que ocurre es que consiguen una caída de la respuesta en frecuencia más pronunciada en frecuencias bajas debido a que permiten más rizado que otros filtros en alguna de sus bandas. Se conocen dos tipos de filtros de Chebyshev los cuales son:

Filtros de Chebyshev de tipo I

Son filtros que únicamente tienen polos, presentan un rizado constante en la banda pasante y presentan una caída monótona en la banda no pasante.

la respuesta en frecuencia es:

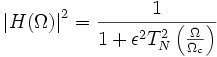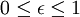
\left | H( \Omega ) \right | ^2 = \frac{1}{1+ \epsilon ^2 T_N ^2 \left ( \frac { \Omega }{ \Omega_c } \right )} para 0 \le \epsilon \le 1

donde N es el orden del filtro, Ωc es la frecuencia de corte, Ω es la frecuencia analógica compleja (Ω=j w) y TN(x) es el polinomio de Chebyshov de orden N, que se define como:

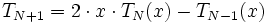T_{N+1}= 2 \cdot x \cdot T_N (x)- T_{N-1} (x) con T0(x) = 1 y T1(x) = x

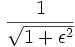En estos filtros la frecuencia de corte no depende de N y el módulo de su respuesta en frecuencia oscila (rizado) entre 1 y 1 \over { \sqrt{1+\epsilon ^2}}.

Filtros de Chebyshev de tipo II

Estos filtros a diferencia de los Chebyshov I presentan ceros y polos, su rizado es constante en la banda no pasante y además presentan una caída monotónica en la banda pasante.

Su respuesta en frecuencia es:

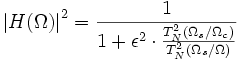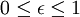
\left | H( \Omega ) \right | ^2 = \frac{1}{1+ \epsilon ^2 \cdot \frac{T_N ^2 \left ( \Omega_s / \Omega_c \right)} {T_N ^2 \left ( \Omega_s / \Omega \right )}} para 0 \le \epsilon \le 1

En un diagrama de circunferencia unidad, los polos estarían en una elipse y los ceros sobre el eje imaginario.

Otros tipos de filtros

Véase también

Obtenido de "Filtro de Chebyshov"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать курсовую

Mira otros diccionarios:

  • Filtro analógico — Saltar a navegación, búsqueda Los filtros analógicos al igual que cualquier otro tipo de filtro, discriminan lo que pasa a su través atendiendo a algunas de sus características. Al tratarse de filtros electrónicos lo que pasa a su través son… …   Wikipedia Español

  • Filtro de Cauer — Saltar a navegación, búsqueda Respuesta de un filtro de Cauer. Un filtro elíptico o filtro de Cauer es un tipo de filtro eléctrico. Su nombre se debe al matemático alemán Wilhelm Cauer, una de las personas que más ha contribuido al desarrollo de… …   Wikipedia Español

  • Polinomio de Chebyshov — Saltar a navegación, búsqueda En matemática, los polinomios de Chebyshov, nombrados en honor a Pafnuti Chebyshov, son una familia de polinomios ortogonales que están relacionados con la fórmula de De Moivre y son definidos de forma recursiva con… …   Wikipedia Español

  • Polinomios de Chebyshov — En matemática, los polinomios de Chebyshov, nombrados en honor a Pafnuti Chebyshov, son una familia de polinomios ortogonales que están relacionados con la fórmula de De Moivre y son definidos de forma recursiva con facilidad, tal como ocurre con …   Wikipedia Español

  • Pafnuti Chebyshov — Pafnuti Lvóvich Chebyshov. Pafnuti Lvóvich Chebyshov (Пафнутий Львович Чебышёв) (16 de mayo de 1821 8 de diciembre de 1894) fue un matemático ruso. Su nombre se translitera también como Tchebychev, Tchebycheff, Tschebyscheff, Chebyshev o Čebišëv …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”