Un filtro digital es un sistema que, dependiendo de las variaciones de las señales de entrada en el tiempo y amplitud, se realiza un procesamiento matemático sobre dicha señal; generalmente mediante el uso de la Transformada rápida de Fourier; obteniéndose en la salida el resultado del procesamiento matemático o la señal de salida.

Los filtros digitales tienen como entrada una señal analógica o digital y en su salida tienen otra señal analógica o digital, pudiendo haber cambiado en amplitud, frecuencia o fase dependiendo de las características del filtro digital.

El filtrado digital es parte del procesado de señal digital. Se le da la denominación de digital más por su funcionamiento interno que por su dependencia del tipo de señal a filtrar, así podríamos llamar filtro digital tanto a un filtro que realiza el procesado de señales digitales como a otro que lo haga de señales analógicas.

Comunmente se usa para atenuar o amplificar algunas frecuencias, por ejemplo se puede implementar un sistema para controlar los tonos graves y agudos del audio del estéreo del auto.

La gran ventaja de los filtros digitales sobre los analógicos es que presentan una gran estabilidad de funcionamiento en el tiempo.

El filtrado digital consiste en la realización interna de un procesado de datos de entrada.

En general el proceso de filtrado consiste en el muestreo digital de la señal de entrada, el procesamiento considerando el valor actual de entrada y considerando las entradas anteriores. El último paso es la reconstrucción de la señal de salida.

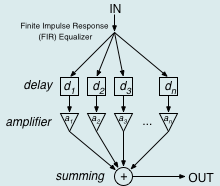
En general la mecánica del procesamiento es:

1. Tomar las muestras actuales y algunas muestras anteriores (que previamente habían sido almacenadas) para multiplicadas por unos coeficientes definidos.
2. También se podría tomar valores de la salida en instantes pasados y multiplicarlos por otros coeficientes.
3. Finalmente todos los resultados de todas estas multiplicaciones son sumados, dando una salida para el instante actual.

El procesamiento interno y la entrada del filtro serán digitales, por lo que puede ser necesario una conversión analógica-digital o digital-analógica para uso de filtros digitales con señales analógicas.

Un tema muy importante es considerar las limitaciones del filtro de entrada debido a Teorema de muestreo de Nyquist-Shannon que en pocas palabras; si quiero procesar hasta una frecuencia de 10KHz, debo muestrear a por lo menos 20 KHz.

Los filtros digitales se usan frecuentemente para tratamiento digital de la imagen o para tratamiento del sonido digital.

Otro ejemplo común de filtros digitales son los programas para retocar imágenes.

Contenido 1 Tipos de filtros 2 Expresión general de un filtro 3 Ejemplo del diseño de un filtro 4 Véase también 5 Referencias 6 Enlaces externos

Tipos de filtros

Hay varios tipos de filtros así como distintas clasificaciones para estos filtros:

• De acuerdo con la parte del espectro que dejan pasar y que atenúan hay:
  • Filtros pasa alto.
  • Filtros pasa bajo.
  • Filtros pasa banda.
    • Banda eliminada.
    • Multibanda.
    • Pasa todo.
    • Resonador.
    • Oscilador.
    • Filtro peine (Comb filter).
    • Filtro ranura o filtro rechaza banda (Notch filter).
• De acuerdo con su orden:
  • primer orden
  • segundo orden
• De acuerdo con el tipo de respuesta ante entrada unitaria:
  • FIR (Finite Impulse Response)
  • IIR (Infinite Impulse Response)
  • TIIR (Truncated Infinite Impulse Response)
• De acuerdo con la estructura con que se implementa:
  • Laticce
  • Varios en cascada
  • Varios en paralelo

Expresión general de un filtro

Hay muchas formas de representar un filtro. Por ejemplo, en función de w (frecuencia digital), en función de z y en función de n (número de muestra). Todas son equivalentes, pero a la hora de trabajar a veces conviene más una u otra. Como regla general se suele dejar el término a₀=1.

Si se expresa en función de z y en forma de fracción:

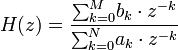
Y en dominio de n:

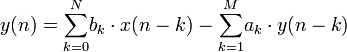
Los coeficientes son los a y b y son los que definen el filtro, por lo tanto el diseño consiste en calcularlos.

Ejemplo del diseño de un filtro

En primer lugar se parte de las especificaciones y, basándose en éstas, se elige el tipo de filtro. En este ejemplo se parte de un filtro digital que anule las frecuencias menores a 5Hz y la de 50Hz y que no altere al resto, la frecuencia de muestreo será 1000Hz, además se quiere fase lineal.

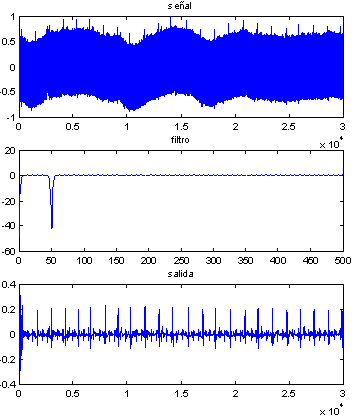
Con estas especificaciones se elige un filtro FIR. El diseño se puede hacer manualmente o con la ayuda de un ordenador. En este ejemplo el método de diseño será el de Remez. En Matlab se obtienen los coeficientes que definen el filtro, que en la ecuación anterior se llaman a y b (el numerador es la variable b y el denominador solo tiene un término que es 1, como corresponde a un filtro FIR):

[n,fo,mo,w]=remezord([0 5 45 50 50 55],[0 1 0 1],[0.01 0.1 0.01 0.1],1000); b = remez(n,fo,mo,w)

En la siguiente figura se muestra el aspecto del filtro en el centro. En la parte superior se muestra la señal que se quiere filtrar y en la parte inferior la señal filtrada (se trata de un electrocardiograma).

El siguiente paso es seleccionar la forma de implementarlo, es decir su estructura. Luego se elige el hardware sobre el que funcionará. Normalmente un Procesador digital de señal o una FPGA, aunque también puede ser un programa de ordenador. Finalmente se usan los coeficientes obtenidos y la estructura elegida para crear el programa.

Véase también

• Filtro analógico
• muestreo, Teorema de muestreo de Nyquist-Shannon, Harry Nyquist
• Conversión analógica-digital
• Conversión digital-analógica
• Fourier, Transformada de Fourier
• Creación rápida de filtros digitales con LabVIEW

Referencias

• [1]
• [2]

Enlaces externos

• Librería para la construcción de filtros digitales con LabVIEW