- Funciones elípticas de Weierstrass
-
En el ámbito de las matemáticas, las funciones elípticas de Weierstrass son un grupo de funciones elípticas que poseen una forma particularmente simple (cf funciones elípticas de Jacobi); han sido designadas en honor al matemático Karl Weierstrass. Esta clase de funciones es también llamada funciones P y generalmente se las escribe utilizando el símbolo
 (que corresponde a una letra P estilizada, llamada P de Weierstrass).
(que corresponde a una letra P estilizada, llamada P de Weierstrass).Contenido
Definiciones
Se puede definir a la función elíptica de Weierstrass de tres maneras muy similares, cada una de ellas posee ciertas ventajas. Una es como una función de variable compleja z y una retícula Λ en el plano complejo. Otra es en término de z y dos números complejos ω1 y ω2 que definen un par de generadores, o períodos, de la retícula. La tercera es en término de z y de un módulo τ en el semiplano superior. Esta se relaciona con la definición previa mediante la siguiente expresión τ = ω2 / ω1, la cual en virtud de la convención usual de pares de períodos se encuentra en el semiplano superior. Utilizando este método, para un z fijo las funciones de Weierstrass resultan ser funciones modulares de τ.
Considerando los dos períodos la función elíptica de Weierstrass es una función elíptica con períodos ω1 y ω2 definida como
Entonces Λ = mω1 + nω2 son los puntos de la retícula de período, por lo que
para todo par de generadores de la retícula define la función de Weierstrass como una función de una variable compleja y una retícula.
Si τ es un número complejo en el semiplano superior, entonces
La suma indicada previamente es homogenea con un grado menos dos, con lo cual se puede definir la función
 de Weierstrass para todo par de períodos, como
de Weierstrass para todo par de períodos, comoBibliografía
- Naum Illyich Akhiezer, Elements of the Theory of Elliptic Functions, (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
- Tom M. Apostol, Modular Functions and Dirichlet Series in Number Theory, Second Edition (1990), Springer, New York ISBN 0-387-97127-0 (See chapter 1.)
- K. Chandrasekharan, Elliptic functions (1980), Springer-Verlag ISBN 0-387-15295-4
- Serge Lang, Elliptic Functions (1973), Addison-Wesley, ISBN 0-201-04162-6
- E. T. Whittaker and G. N. Watson, A course of modern analysis, Cambridge University Press, 1952, chapters 20 and 21
- Konrad Knopp, Funktionentheorie II (1947), Dover; Republished in English translation as Theory of Functions (1996), Dover ISBN 0-486-69219-1
- Abramowitz and Stegun, chapter 18
Referencias
Enlaces externos
- Weisstein, Eric W. «Weierstrass Elliptic Function» (en inglés). MathWorld. Wolfram Research.
- Funciones elípticas, página de análisis complejo de Hans Lundmark.
Categorías:- Formas modulares
- Curvas algebraicas
- Funciones elípticas
Wikimedia foundation. 2010.


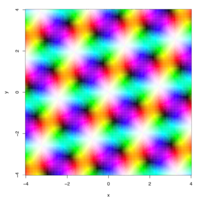
 Notar la retícula regular de los polos, y dos retículas que se entrecruzan de ceros.
Notar la retícula regular de los polos, y dos retículas que se entrecruzan de ceros.


