Gráfico Q-Q

Gráfico Q-Q
A normal Q-Q plot of randomly generated exponential(1) data.
A normal Q-Q plot of randomly generated normal(0,1) data.

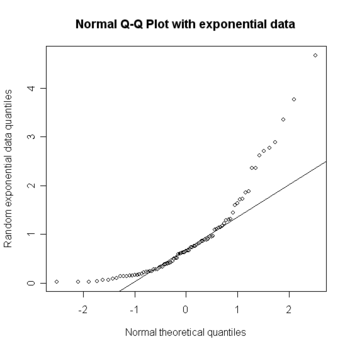
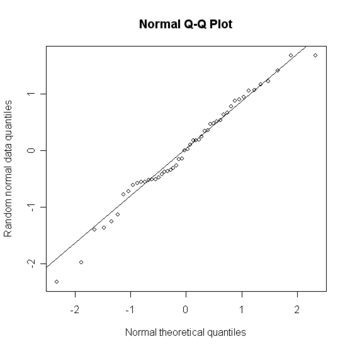
En estadística, un gráfico Q-Q ("Q" viene de cuantil) es un método gráfico para el diagnóstico de diferencias entre la distribución de probabilidad de una población de la que se ha extraído una muestra aleatoria y una distribución usada para la comparación. Una forma básica de gráfico surge cuando la distribución para la comparación es una distribución teórica.[1] No obstante, puede usarse la misma idea para comparar las distribuciones inferidas directamente de dos conjuntos de observaciones, donde los tamaños de las muestras sean distintos.[2]

Un ejemplo del tipo de diferencias que pueden comprobarse es la no-normalidad de la distribución de una variable en una población. Para una muestra de tamaño n, se dibujan n puntos con los (n+1)-cuantiles de la distribución de comparación, por ejemplo, la distribución normal, en el eje horizontal el estadístico de k-ésimo orden, (para k = 1, ..., n) de la muestra en el eje vertical. Si la distribución de la variable es la misma que la distribución de comparación se obtendrá, aproximadamente, una línea recta, especialmente cerca de su centro. En el caso de que se den desviaciones sustanciales de la linealidad, los estadísticos rechazan la hipótesis nula de similitud.

Contenido

Representación gráfica

Para los cuantiles de la distribución de comparación se usa habitualmente la fórmula \frac{k}{n+1}. Hay varias fórmulas diferentes que se han usado o propuesto para representaciones gráficas simétricas. Tales fórmulas tienen la forma \frac{k-a}{n+1-2a}, para algún valor de a entre 0 y \frac{1}{2}. La expresión de arriba, \frac{k}{n+1} es sólo un ejemplo de estas fórmulas, para a = 0. Otras expresiones incluyen:

Para grandes tamaños muestrales, n, hay muy poca diferencia entre todas estas expresiones.

Relación con gráficas de probabilidad

Los gráficos Q-Q son similares a los gráficos de probabilidad (que para una distribución normal se llaman gráficos de probabilidad normal o gráficos rankit). La diferencia es que en un gráfico de probabilidad, en lugar de usar el cuantil de la distribución como eje X, se usa la esperanza matemática del estadístico de k-ésimo orden de la distribución. Sólo cuando n es pequeño hay una diferencia sustancial entre un gráfico Q-Q y un gráfico de probabilidad.

Véase también

  • Análisis Probit, desarrollado por Chester Ittner Bliss en 1934.

Notas

  1. ↑ Gnanadesikan (1977) p199.
  2. ↑ Cleveland (1994), p144.
  3. ↑ A simple (and easy to remember) formula for plotting positions.
  4. ↑ Engineering Statistics Handbook: Normal Probability Plot Nótese que aquí también se usa una expresión diferente para el primer y último puntos. [1] cita el trabajo original de Filliben, en 1975.
  5. ↑ Distribution free plotting position, Yu & Huang
  6. ↑ Esta es una aproximación inicial de Blom en 1953 y se trata de la expresión usada en Minitab.
  7. ↑ Esta gráfica fue usada por Gringorten en 1963 para dibujar puntos en tests de la distribución de Gumbel.

Referencias

  • Cleveland, W.S. (1994) The Elements of Graphing Data, Hobart Press ISBN 0-9634884-1-4
  • Gnanadesikan, R. (1977) Methods for Statistical Analysis of Multivariate Observations, Wiley ISBN 0-471-30845-5.
  • Wilk, M.B., Gnanadesikan, R. (1968) Probability plotting methods for the analysis of data. Biometrika, 55, 1–17.

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Gráfico — Saltar a navegación, búsqueda Gráfico puede designar: Como sustantivo, a la representación de datos por medio de líneas: En matemáticas y todo tipo de ciencias, naturales y sociales, gráfico o gráfica es la representación visual de la variación… …   Wikipedia Español

  • gráfico — gráfico, ca adjetivo 1. De la escritura o de la imprenta. artes* gráficas. periodista* gráfico. reportaje* gráfico. reportero* gráfico. 2. Que se representa con signos, figuras, líneas o dibujos: representación gráfica, descripción gráfica. En el …   Diccionario Salamanca de la Lengua Española

  • gráfico — gráfico, ca (Del lat. graphĭcus, y este del gr. γραφικός). 1. adj. Perteneciente o relativo a la escritura y a la imprenta. 2. Dicho de una descripción, de una operación o de una demostración: Que se representa por medio de figuras o signos. U. t …   Diccionario de la lengua española

  • -grafico — [dal gr. graphikós ]. Secondo elemento con cui sono formati gli aggettivi derivati dai sostantivi in grafia o in grafo : biografico, cinematografico, monografico, tipografico, ecc …   Enciclopedia Italiana

  • grafico — / grafiko/ [dal lat. graphĭcus, agg., che riguarda la scrittura o il disegno ] (pl. m. ci ). ■ agg. 1. [che concerne l immagine, il disegno, la rappresentazione e sim.] ▶◀ ‖ iconografico. 2. (bibl.) [che si riferisce in generale all arte della… …   Enciclopedia Italiana

  • gráfico — adj. 1. Relativo à grafia. 2. Diz se de tudo o que se refere à arte de representar os objetos por linhas ou figuras. 3. Relativo à arte de reproduzir pela tipografia, gravura, estereotipia, etc. • s. m. 4. Traçado linear da marcha de um fenômeno… …   Dicionário da Língua Portuguesa

  • gráfico — (Del lat. graphicus < gr. graphikos, referente a la escritura o al dibujo.) ► adjetivo 1 ARTES GRÁFICAS Que está relacionado con la escritura o con la imprenta: ■ artes gráficas. 2 Que se expresa utilizando dibujos o signos no lingüísticos: ■… …   Enciclopedia Universal

  • grafico — grà·fi·co agg., s.m. CO 1. agg., che riguarda la grafia, la scrittura: segno grafico 2. agg., che consiste in un disegno: rappresentazione grafica 3. agg., che riguarda l arte, la tecnica della stampa: industria grafica 4. agg. TS inform. che fa… …   Dizionario italiano

  • gráfico — adj 1 Que pertenece a la escritura, la imprenta, el dibujo, etc o se relaciona con ellos: signo gráfico, artes gráficas 2 Que está hecho a base de dibujos, fotografías, etc: guía gráfica, manual gráfico 3 Que es muy claro: un templo gráfico, una… …   Español en México

  • gráfico — {{＃}}{{LM G19285}}{{〓}} {{SynG19781}} {{［}}gráfico{{］}}, {{［}}gráfica{{］}} ‹grá·fi·co, ca› {{《}}▍ adj.{{》}} {{＜}}1{{＞}} De la escritura y de la imprenta o relacionado con ellas: • Estudia artes gráficas.{{○}} {{＜}}2{{＞}} {{♂}}Referido a la forma… …   Diccionario de uso del español actual con sinónimos y antónimos

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”