Simetría

Simetría
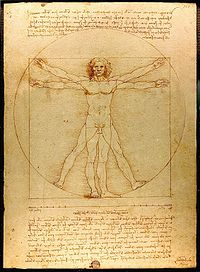El hombre Vitrubio, de Leonardo da Vinci (ca. 1487), es una representación frecuente de la simetría del cuerpo humano, y por extensión del mundo natural.

La simetría es un rasgo característico de formas geométricas, sistemas, ecuaciones y otros objetos materiales, o entidades abstractas, relacionada con su invariancia bajo ciertas transformaciones, movimientos o intercambios.

En condiciones formales, decimos que un objeto es simétrico en lo que concierne a una operación matemática dada, si, cuando aplicado al objeto, esta operación no cambia el objeto o su aspecto. Dos objetos son simétricos uno al otro en lo que concierne a un grupo dado de operaciones si uno es obtenido de otro por algunas operaciones (y viceversa). En la geometría 2D las clases principales de simetría de interés son las que conciernen a las isometrías de un espacio euclídeo: traslaciones, rotaciones, reflexiones y reflexiones que se deslizan.

La simetría también se encuentra en organismos vivos.

Contenido

Simetría en geometría

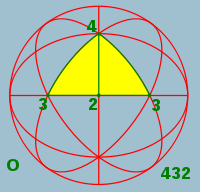Grupo de simetría de la esfera.

Cuando hablamos de objetos físicos o elementos geométricos el concepto de simetría está asociado a transformaciones geométricas tales como las rotaciones, las reflexiones o las traslaciones. Dos simetrías sencillas son la simetría axial y la simetría central. Así se dice que un objeto presenta:

  • Simetría esférica si existe simetría bajo algún grupo de rotaciones, matemáticamente equivale a que el grupo de simetría de un objeto físico o entidad matemática sea SO(3).
  • Simetría cilíndrica o simetría axial si existe un eje tal que los giros alrededor de él no conducen a cambios de posición en el espacio, matemáticamente está asociado a un grupo de isometría SO(2).
  • Simetría reflectiva o simetría especular que se caracteriza por la existencia de un único plano, matemáticamente está asociado al grupo SO(1) o su representación equivalente \mathbb{Z}_2. En dos dimensiones tiene un eje de simetría y en tres dimensiones tiene un plano. El eje de simetría de una figura bidimensional es una línea, si se construye una perpendicular, cualquier punto que reposee en esta perpendicular a la misma distancia del eje de simetría son idénticos. Otra manera de verlo es que si la forma se doblara por la mitad sobre el eje, las dos mitades serían iguales. Por ejemplo, un cuadrado tiene cuatro ejes de simetría, ya que hay cuatro formas diferentes de doblarlo haciendo que sus bordes coincidan. Un círculo tendría infinitos ejes de simetría por la misma razón.
  • Simetría traslacional se da cuando la transformación T_a(p) = p + a\, deja invariable a un objeto bajo un grupo de traslaciones discretas o continuas. El grupo es discreto si la invariancia sólo se da para un número numerable de valores de a y continuo si la invariancia se presenta para un conjunto infinito no numerable de valores de a en caso contrario.

Algunos tipos de simetría que combinan dos o más de los anteriores tipos son:

  • Simetría antitraslacional que implica una reflexión en una línea o plano combinado con una traslación a lo largo de ese mismo eje. El grupo de simetría es isomorfo a \mathbb{Z}_2\times \R^n.
  • Simetría de rotorreflexión o simetría de rotación impropia, implica rotación al rededor de un eje combinado con reflexión en un eje perpendicular al de rotación.
  • Simetría helicoidal implica un movimiento de rotación en torno a un eje dado con un movimiento de traslación a lo largo de ese mismo eje. Puede ser de tres clases:
    1. Simetría helicoidal infinita
    2. Siemtría helicoidal de n-ejes
    3. Siemtría helicoidal que no se repite

Simetría en física

En física el concepto de simetría puede formularse en una forma no geométrica. Si K es un conjunto de objetos matemáticos del mismo tipo (funciones, formas geométricas, ecuaciones, ...) y G es un grupo de transformaciones que actúa sobre K de tal manera que:

g (\in G): K \to K

Se dice que un elemento de k0 presenta simetría si:[1]

\forall g\in G: g(k_0) = k_0

Así por ejemplo varias leyes de conservación de la física son consecuencia de la existencia de simetrías abstractas del lagrangiano, tal como muestra el teorema de Noether. En ese caso K representaría el conjunto de lagrangianos admisibles, k0 el lagrangiano del sistema bajo estudio y G puede representar traslaciones espaciales (conservación del momento lineal), traslaciones temporales (conservación de la energía), rotaciones (conservación del momento angular) u otro tipo de simetrías abstractas (conservación de la carga eléctrica, el número leptónico, la paridad, etc.)

  • Ejemplo 1. Como primer ejemplo consideremos un electrón moviéndose entre dos placas infinitas cargadas uniformemente (dicho sistema se aproxima cierto tipo de condensadores), dado que cualquier traslación paralela a los planos constituye una simetría del sistema físico, entonces tanto la fuerza paralela a dichos planos es nula y por tanto la velocidad paralela a los planos es constante.
  • Ejemplo 2. Consideremos un satélite orbitando alrededor de un astro (planeta o estrella) con simetría esférica perfecta, consideremos además que la velocidad del satélite sea perpendicular a la línea entre el centro del satélite y el astro. En ese caso, el lagrangiano es totalmente invariante respecto a rotaciones según un eje que pase por el centro de la fuente del campo gravitatorio. En este caso debido a la simetría de rotación tanto del lagrangiano como de las condiciones iniciales del movimiento, la velocidad perpendicular al planeta es constante y la trayectoria es un círculo invariante bajo una rotación perpendicular al plano de la órbita.

Estos dos ejemplos anteriores son casos del teorema de Noether, un resultado general que establece que si existe un grupo uniparamétrico de simetría G para el lagrangiano tal que:

No se pudo entender (La conversión a PNG ha sido errónea): \forall \phi_\lambda\in G: L(\phi_\lambda(\mathbf{q}),\phi_\lambda(\dot\mathbf{q}),t) = L(\mathbf{q},\dot\mathbf{q},t)

Entonces la cantidad escalar:

No se pudo entender (La conversión a PNG ha sido errónea): \left \langle \left . \frac{d\phi_\lambda}{d\lambda}\right \vert_{\lambda=0}, \frac{dL}{d\dot\mathbf{q}}\right\rangle = v_1p_1 + ... + v_Np_N

Siendo v el campo vectorial que general el grupo uniparamétrico de transformaciones de simetría, y pi los momentos conjugados de las coordenadas generalizadas de posición.

Simetría en química

Artículo principal: Simetría molecular

En química la simetría geométrica de las moléculas es importante, particularmente en química orgánica. Además propiedades como su momento dipolar y las transiciones espectroscópicas permitidas (basadas en reglas de selección como la regla de Laporte) pueden predecirse o ser explicadas a partir de la simetría de la molécula. Las simetrías que aparecen en química están asociadas a grupos finitos de isometrías, en concreto son grupos puntuales de transformaciones de isometría.

Simetría en biología

Ilustración de los distintos tipos de simetría en las formas orgánicas (Field Museum, Chicago).

Simetría en biología es la equilibrada distribución en el cuerpo de los organismos de aquellas partes que aparecen duplicadas. Los planes corporales de la mayoría de organismos pluricelulares exhiben alguna forma de simetría, bien sea simetría radial o simetría bilateral. Una pequeña minoría no presenta ningún tipo de simetría (son asimétricos).

Simetría radial

Artículo principal: Simetría radial (biología)

La simetría radial es la simetría definida por un eje heteropolar (distinto en sus dos extremos). El extremo que contiene la boca se llama lado oral, y su opuesto lado aboral o abactinal. Sobre este eje, se establecen planos principales de simetría; dos perpendiculares que definen las posiciones per-radiales. Las estructuras en otros planos (bisectrices de los per-radiales) quedan en posiciones inter-radiales. La zona entre los per-radiales y los inter-radiales es la zona ad-radial.

Simetría bilateral

Simetria-bilateria.svg

Artículo principal: Simetría bilateral

La mayoría de especies animales tiene simetría bilateral y pertenece por tanto al grupo Bilateria, aunque hay especies como los erizos y las estrellas de mar que presentan simetría radial secundaria (las fases de desarrollo tempranas y las larvas poseen simetría bilateral que posteriormente se pierde en el adulto). La simetría bilateral permite la definición de un eje corporal en la dirección del movimiento, lo que favorece la formación de un sistema nervioso centralizado y la cefalización.

Simetría en música

En música clásica, existen composiciones en las que podemos encontrar distribuciones de las notas generadas mediante simetría bilateral, traslación o giros de media vuelta. Algunos ejemplos de composiciones, son: el Preludio de Johann Sebastian Bach, la Sonata en G mayor de Domenico Scarlatti, Lotosblume de Robert Schumann, o Die Meiestersinger de Richard Wagner.

Simetría en alimentación de AC

En el contexto de la electrónica de radiofrecuencia, se habla de una alimentación simétrica de AC cuando ninguno de los conductores está a la masa. Cuando uno de los conductores está a la masa y el otro experimenta las variaciones de tensión, se dice que la alimentación es asimétrica.

Existen importantes aplicaciones tecnológicas basadas en la alimentación simétrica, ya que la alimentación simétrica tiene la gran ventaja de que la pérdida de potencia en la línea de transmisión es un orden de magnitud menor que la alimentación asimétrica por cable coaxial.

  • En efecto, el campo alterno generado por el conductor ascendente es cancelado por el campo generado por su homólogo descendente.
  • Además, la alimentación simétrica en delta permite la simplificación de la construcción.

La alimentación simétrica es por lo tanto la alimentación preferida en la operación QRP y en el modo EME, modos donde cada dB de ganancia cuenta.

Ver también

Simetría en estadística

Simetría en juegos y puzzles

Simetría en literatura

Simetría moral

Simetría en física

Otros

Referencias

  1. ↑ Wald, 1984, p. 441-444.

Bibliografía

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?
Sinónimos:
, , , , , , , , , , , ,


Antónimos:
desequilibrio, desproporción


Mira otros diccionarios:

  • simetría — sustantivo femenino 1. (no contable.) Disposición de varias cosas, o de varias partes de una cosa, colocadas de tal modo que dos o más se corresponden en posición, forma y dimensiones a uno y otro lado de un punto, de un eje o de un plano, como… …   Diccionario Salamanca de la Lengua Española

  • simetría — (Del lat. symmetrĭa, y este del gr. συμμετρία). 1. f. Correspondencia exacta en forma, tamaño y posición de las partes de un todo. 2. Biol. Correspondencia que se puede distinguir, de manera ideal, en el cuerpo de una planta o de un animal… …   Diccionario de la lengua española

  • simetría — (en anatomía) correspondencia de dos estructuras situadas en lados opuestos del organismo, o igualdad entre las partes a cada lado de una línea divisoria. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A.… …   Diccionario médico

  • simetria — s. f. Relação de tamanho ou de disposição que entre si devem ter as coisas ou as partes de um todo em relação a um ponto, eixo ou plano …   Dicionário da Língua Portuguesa

  • Simetría — (Del gr. symmetria < syn , conjuntamente + metron, medida.) ► sustantivo femenino 1 Modo de estar colocadas las cosas de un conjunto, de tal forma que existen dos partes exactamente iguales, que se contraponen. ANTÓNIMO asimetría 2 BOTÁNICA,… …   Enciclopedia Universal

  • simetría — s f 1 Relación de equilibrio, correspondencia o igualdad que existe entre la forma, el tamaño, la distribución, el color, etc, de dos cosas o partes de una misma cosa: simetría de un cuadro, simetría de fuerzas 2 Simetría bilateral La que se… …   Español en México

  • simetría — {{＃}}{{LM S35792}}{{〓}} {{SynS36684}} {{［}}simetría{{］}} ‹si·me·trí·a› {{《}}▍ s.f.{{》}} Regularidad en la disposición de las partes de un cuerpo de modo que se corresponden en posición, forma y dimensiones a uno y otro lado de un punto, de un eje …   Diccionario de uso del español actual con sinónimos y antónimos

  • simetría — (f) (Intermedio) posición igual de los elementos con respecto a un eje o centro Ejemplos: La organización de la habitación de los hermanos se basaba en la simetría. La simetría en el rostro de la modelo la hace muy bella. Sinónimos: relación,… …   Español Extremo Basic and Intermediate

  • Simetría molecular — Simetría del agua. En química, la simetría molecular describe la simetría de las moléculas y utiliza este criterio para su clasificación. La simetría molecular es un concepto fundamental en química, pues muchas de las propiedades químicas de una… …   Wikipedia Español

  • Simetría bilateral — en el ser humano. En biología, dice qe simetría es la equilibrada distribución en el cuerpo de los organismos de aquellas partes que aparecen duplicadas. Los planos corporales de la mayoría de organismos pluricelulares exhiben alguna forma de… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”