Ejemplo de analema solar, mostrando la curva en forma de 'ocho' tumbado

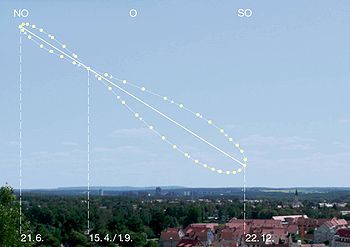
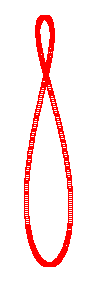
En astronomía, el analema (en inglés analemma, con dos emes) es la curva que describe la posición del Sol en el cielo si todos los días del año se lo observa a la misma hora del día (tiempo civil) y desde el mismo lugar de observación. El analema forma una curva que suele ser, aproximadamente, una forma de ocho (8) o leminiscata. Pueden observarse analemas en otros planetas del Sistema Solar, pero poseen una forma diferente al observado en la Tierra, pudiendo llegar a ser curvas diferentes de un ocho (en Marte es muy similar a una gota de agua), aunque poseen como característica común: ser siempre cerradas. El componente axial del analema muestra la declinación del Sol mientras que la componente transversal ofrece información acerca de la ecuación de tiempo (que es la diferencia entre el tiempo solar aparente y el tiempo solar medio). A veces, se dibuja en los globos terráqueos.

Observación de analemas

Astrofotografía

Es posible obtener un analema poniendo una cámara fotográfica fija (mediante un trípode) apuntando a una posición dada en el cielo (a ser posible un punto de la eclíptica) y cuando pase el Sol por el centro sacar una foto; tras 24 horas se repite la operación, sobre imprimiendo la foto del día anterior, y se repite el procedimiento para cada día del año. De esta forma se obtiene una foto con una especie de 8 que representa un analema. Los analaemas son un sujeto importante de la astrofotografía.^[1] Una imagen que incluye un eclipse total de sol en una de sus imágenes se denomina Tutulema^[2]

Proyección gnomónica

Ejemplo de diseño de reloj con el trazado del sistema horario civil, se puede ver cómo cada una de las horas representa un analema.

Otra forma más sencilla es empleando una vara o estaca clavada en el suelo, sobre una superficie con la que se pueda hacer marcas estables a lo largo de un intervalo de tiempo de un año. La estaca tendrá una cierta altura h y su extremo arrojará una sombra que acaba en un extremo; si se toma a una cierta hora la posición de la sombra, y se repite cada 24 horas la misma operación, se obtendrá la proyección gnomónica del analema para ese instante. Esta proyección permite crear un tipo de relojes solares denominado reloj solar de tiempo civil, donde las líneas rectas de la escala se convierten en "ochos" para cada hora de tiempo civil.^[3]

Proyección estereográfica

Una variante de esta forma de representar un analema es reprentándola en el cristal de una ventana (por ejemplo), fijado un punto de observación marcar cada 24 horas la posición del Sol vista desde el punto de observación ya pre-fijado el primer día y repetir la operación cada 24 horas. El resultado es una analema proyectada estereográficamente sobre la ventana.

Etimología

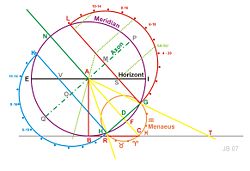
La palabra "analemma" procede del griego para indicar el pedestal de un reloj de sol, y proviene del verbo griego "analambanein", que significa "llevar, reanudar, reparar" el analema es el pedestal que soporta al reloj de sol sobre él. Antiguamente la palabra "analema" aparece en ciertos tratados de gnomónica relacionada con la forma especial de construir un reloj de sol, abatiendo las circunferencias notables de tal forma que se tiene una proyección ortográfica sobre el plano del reloj.^[4] Para los antiguos (hasta bien entrado el siglo XVIII) la palabra analema significaba el procedimiento de construcción geométrica de relojes de sol, este método fue demostrado geométricamente y revisado completamente por el matemático alemán Christoph Clavius, 1537-1612,^[5] Posteriormente este concepto fue cambiando a lo largo de la historia hasta el concepto con el que se entiende hoy en día.^[6]

Historia

Analema de Vitrubio, tal y como lo describe en el Libro IX de su "Re achitectura".

Ya en la Edad Media la necesidad de determinar el instante del equinocio para determinar los primeros analemas que se calcularon Paolo del Pozzo Toscanelli que el año 1475, se emplearon el diseño de una de las primeras meridianas capaces de proporcionar con gran precisión no sólo el evento del mediodía, sino que se era capaz de determinar la época del año. Esta meridiana fue construida en la catedral de Santa María del Fiore, Florencia, Italia.^[7] La meridiana se construyó sobre el suelo en forma de una tira de mármol de gran longitud y en una pared meridional se practicó un agujero que permitera pasar un 'punto' luminoso sobre la tira de marmol indicando en una escala la fecha del año, el método de construcción de estas meridianas fue mediante un procedimiento geométrico antiguo denominado "analema".

Los avances mecánicos del siglo XVIII hicieron que los relojes mecánicos fueran cada vez más precisos, y con la llegada de los relojes de péndulo fue posible medir minutos de tiempo con gran precisión. En este instante se empezó a percibir la diferencia entre hora solar (medida por los relojes solares) y el tiempo civil (medida por las regulares maquinarias de los relojes mecánicos), la que está dada por la ecuación de tiempo. Es posible que fuera por esta fecha cuando la palabra analema se fuera confundiendo poco a poco, del procedimiento de la gnomónica a la representación en el espacio de la figura

Características

Tres parámetros orbitales afectan la forma y el tamaño del analema: la oblicuidad (23.45°), la excentricidad, y el ángulo del equinoccio con respecto del periápside.

Referencias

Véase también

• Ecuación del tiempo

Enlaces externos

• Discusión sobre las desviaciones de esta curva
• Astronomy Picture of the Day, 2002 9 de julio: Analema
• Astronomy Picture of the Day, 2003 20 de marzo: Analemma de Orto
• Astronomy Picture of the Day, 2004 21 de junio: Analema sobre la antigua Nemea
• Astronomy Picture of the Day, 2005 13 de junio: Analema de la luna
• Astronomy Picture of the Day, 2006 23 de diciembre: Analemma over the Temple of Olympian Zeus
• Astronomy Picture of the Day, 2006 30 de diciembre: Analema marciano en el "Sagan Memorial Station" (simulado)
• Astronomy Picture of the Day, 2007 17 de junio: Analema sobre Ucraina
• Astronomy Picture of the Day, 2007 2 de octubre: Tutulemma: Analema de un eclipse solar
• Series de analemas desde el amanecer hasta el atardecer
• Explicación de un analema por John Holtz
• Foto de "Earth Science Photo of the Day", 22 de enero de 2005
• "The Equation of Time and the Analemma", por Kieron Taylor
• Un artículo de Brian Tung, que contiene un enlace a un programa en lenguaje C que emplea una fórmula precisa (muy precisa particularly at high inclinations and eccentricities)
• The Analemma for Latitudinally-Challenged People explains rising and setting analemmas as viewed from different latitudes. It provides more depth than most analemma sources. PDF format. 1,433 Kb.
• Analemma.com is dedicated to the analemma.
• Calculate and Chart the Analemma is a web site offered by a Fairfax County Public Schools planetarium that describes the analemma and also offers a downloadable spreadsheet that allows the user to experiment with analemmas of varying shapes.