El objetivo del Analisis modal en la mecánica estructural es determinar las formas modales naturales y frecuencias de un objeto o estructura durante vibración libre. Es común usar el Método de los elementos finitos (FEM) para desempeñar el análisis porque, como otros cálculos usando el FEM, el objeto que se analiza puede tener formas arbitrarias y los resultados de los cálculos son aceptables. Los tipos de ecuaciones las cuales surgen del analisis modal son esas vistas en Sistemas propios. La interpretacion física de los valores propios y vectores propios las cuales vienen de resolver los sistemas son esas que representan las frecuencias y formas modales correspondientes. A veces, las únicas modalidades deseadas son las menores frecuencias porque ellas pueden ser las modalidades más prominentes a las cuales el objeto vibrara, dominando todas las modalidades mayores de frecuencias.

Esto es también posible para probar un objeto físico para determinar sus frecuencias naturales y las formas modales. A esto se denomina analisis modal experimental. Los resultados de las pruebas físicas pueden usarse para calibrar un modelo de elemento finito para determinar si las hipótesis subyacentes hechas fueron correctas (por ejemplo, propiedades correctas de materiales y condiciones límites que fueron usadas).

Contenido 1 Sistemas propios FEA 1.1 Comparacion al algebra lineal 2 Metodos de solucion 3 Ejemplo 4 Véase también

Sistemas propios FEA

Para los problemas mas básicos envolviendo un material linealmente elástico el cual obedece la Ley de elasticidad de Hooke, las ecuaciones de matriz tomando la forma de un sistema de masas de resorte tridimensional dinamico. La ecuación generalizada de movimiento es dada como:

Donde [M] es la matriz de masa, es la 2a derivada de tienpo del desplazamiento [U] (i.e., la aceleracion), es la velocidad, [C] es una matriz de amortiguacion, [K] es la matriz de rigides, y [F] es el vector fuerza. El problema general, con la amortiguacion diferente de cero, es un problema de valor propio cuadratico. Sin embargo, para analisis modal vibracional, la amortiguacion es generalmente ignorada, dejando solo el 1er y 3er termino en el lado izquierdo:

Esta es la forma general de los sistemas propios encontrados en ingenieria estructural usando el Método de los elementos finitos. Adicionalmente, el movimiento armonico es tipicamente asumido para la estructura que si es tomada a ser igual λ[U], donde λ es un valor propio (con unidades de cuadrado de tiempo reciproco, e.g., s ^{− 2}), y la ecuacion se reduce a:

[M][U]λ + [K][U] = [0]

en contraste, la ecuacion para el problema estatico es:

[K][U] = [F]

La cual es esperada cuando todos los terminos teniendo un tiempo derivativo son fijados a cero.

Comparacion al algebra lineal

En Álgebra lineal, es mas comun ver la forma estandar de un sistema propio el cual es expresado como:

[A][x] = [x]λ

Ambas ecuaciones pueden ser vistas como la misma porque si la ecuacion general es multiplicada por el inverso de la masa, [M] ^{− 1}, tomara la forma de este ultimo. deberia notarse que los modos inferiores son deseados, resolviendo el sistema mas probablemente envolveria el equivalente de multiplicando por el inverso de la rigidez, [K] ^{− 1}, un proceso llamado iteraccion inversa. Cuando esto es echo, los valores propios resultantes, μ, relacionan a aquel del original por:

pero los vectores propios son los mismos.

Metodos de solucion

Para problemas linealmente elasticos que son correctamente creados (sin rotacion o ttraslacion de cuerpo rigido), las matrices de rigidez y masa y el sistema en general son positivos definidos. Estas son las matrices mas faciles para tratar con falta algo porque los metodos numericos comunmente aplicados son garantizados para converger a una solucion. Cuando todas las cualidades del sistema son consideradas:

1. Solo los pequeños valores proios y vectores propios de los bajos modos son deseados
2. Las matrices de masa y rigidez son dispersas y altamente bandeadas
3. El sistema es positivo definitivo

una descripcion tipica de la solucion es primero para tridiagonalzar el sistema usando el Algoritmo de Lanczos. Despues, usa el Algoritmo QR para encontrar los vectores propios y valores propios de este primer sistema tridiagonal. Si la iteraccion inversa es usada, los nuevos valores propios seran relacionados a los viejos por 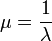, mientras los vectores propios de el original pueden ser calculados de aquellos de las matrices tridiagonalizadas por:

[rⁿ] = [Q][vⁿ]

donde [rⁿ] es un vector Ritz aproximadamente igual a el vector propio de el sistema original, [Q] es la matriz de vectores Lanczos, y [vⁿ] es el n^th vector propio de la matriz tridiagonal.

Ejemplo

La malla mostrada abajo es el marco de un edificio modelado como elementos viga, especificamente conssitiendo de 930 elementos y 385 puntos nodales. La edificacion esta limitada a su base donde los desplazamientos y rotaciones son cero. Las siguientes imagenes son esas de los primeros 5 modos bajos de esta edificacion durante vibracion libre. Este problema puede ser visto como una representacion de las probables defleciones que un edificion tamaria durante un sismo . Como es esperado, el primer modo es un balanceo de el edificio desde el frente hacia atras. El siguiente modo es un balanceo del edificio lado a lado. El tercer modo es un modo de estiramiento y compresion en la vertical direccion y . Para el cuarto modo, el edificio cercanamente asume la forma de una honda senoidal. El quinto modo es un modo de torcion.

Véase también

• Método de los elementos finitos
• Método de los elementos finitos en la mecánica estructural
• analisis modal
• Analisis sismico
• Dinamica estructural
• Vector propio y valor propio
• Modo normal
• Problema de valor propio cuadratico
• Analisis modal para simulacion de deformacion