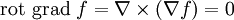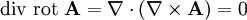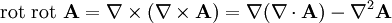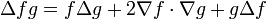Tabla en coordenadas cilíndricas y esféricas
- Tabla en coordenadas cilíndricas y esféricas
-
Tabla en coordenadas cilíndricas y esféricas
Esta es una lista de algunas fórmulas de cálculo vectorial de empleo corriente trabajando con varios sistemas de coordenadas.
Véase también
- Coordenadas curvilíneas
- Campos vectoriales en coordenadas cilíndricas y esféricas
Categorías: Álgebra lineal | Análisis real | Sistemas de coordenadas
Wikimedia foundation.
2010.
Mira otros diccionarios:
Tabla en coordenadas cilíndricas y esféricas — Esta es una lista de algunas fórmulas de cálculo vectorial de empleo corriente trabajando con varios sistemas de coordenadas … Enciclopedia Universal
Anexo:Tabla en coordenadas cilíndricas y esféricas — Esta es una lista de algunas fórmulas de cálculo vectorial de empleo corriente trabajando con varios sistemas de coordenadas. Operación coordenadas cartesianas (x,y,z) coordenadas cilíndricas (ρ,φ,z) coordenadas esféricas (r,θ,φ) Definición de… … Wikipedia Español
Sistema de coordenadas — Un sistema de coordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un espacio euclídeo o más generalmente variedad diferenciable. En física se usan normalmente sistemas de coordenadas… … Wikipedia Español
Coordenadas polares — Localización de un punto en coordenadas polares. El sistema de coordenadas polares es un sistema de coordenadas bidimensional en … Wikipedia Español
Rotacional — Saltar a navegación, búsqueda En el cálculo vectorial, el rotacional o rotor es un operador vectorial que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto. Contenido 1 Introducción 1.1 Fuente vectorial y escalar … Wikipedia Español
Nabla — ∇ El símbolo nabla. El arpa, el instrumento que da nombre al símbolo nabla. En geometría diferencial, nabla (también llamado del) es un operador diferencial representado por el símbolo: ∇ | … Wikipedia Español
Átomo de hidrógeno — Este artículo o sección tiene un estilo difícil de entender para los lectores interesados en el tema. Si puedes, por favor edítalo y contribuye a hacerlo más accesible para el público general, sin eliminar los detalles técnicos que interesan a… … Wikipedia Español
Fresadora — universal con sus accesorios … Wikipedia Español
Constante elástica — Una constante elástica es cada uno de los parámetros físicamente medibles que caracterizan el comportamiento elástico de un sólido deformable elástico. A veces se usa el término constante elástica también para referirse a los coeficientes de… … Wikipedia Español
Free viewpoint television — Saltar a navegación, búsqueda Contenido 1 Introducción 2 Sistema FTV 3 Adquisition of FTV Signal (Adquisición de la Señal FTV) … Wikipedia Español
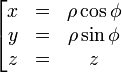
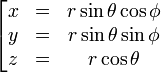
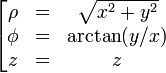
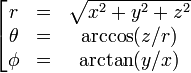
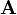
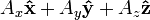
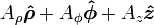
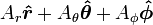
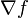
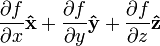
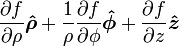
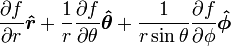
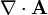
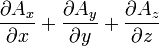
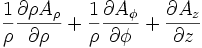
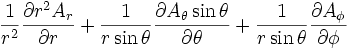
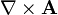
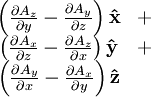
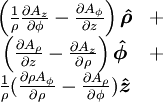
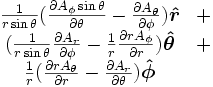
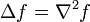
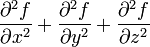
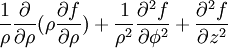
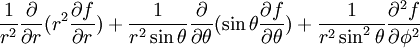
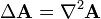
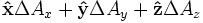
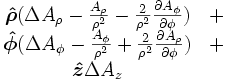
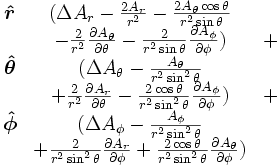
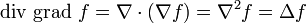 (laplaciano)
(laplaciano)