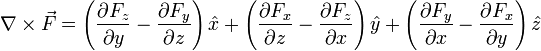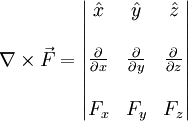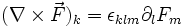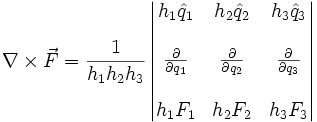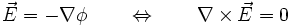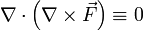Rotacional

Rotacional

Rotacional

En el cálculo vectorial, el rotacional o rotor es un operador vectorial que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto.

Contenido

Introducción

Matemáticamente, esta idea se expresa como el límite de la circulación del campo vectorial, cuando la curva sobre la que se integra se reduce a un punto:

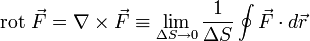
\mbox{rot}\ \vec F = \nabla\times\vec F \equiv \lim_{\Delta S\to 0} \frac{1}{\Delta S}\oint \vec F\cdot d\vec r

Aquí, ΔS es el área de la superficie apoyada en la curva C, que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a ΔS y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

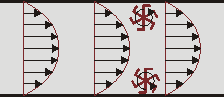
Aunque el que el rotacional de un campo alrededor de un punto sea distinto de cero no implica que las líneas de campo giren alrededor de ese punto y lo encieren. Por ejemplo, el campo de velocidades de un fluido que circula por una tubería (conocido como perfil de Poiseuille) posee un rotacional no nulo en todas partes, salvo el eje central, pese a que la corriente fluye en línea recta:

Poiseuille profile.png

La idea es que si colocamos una rueda de paletas infinitamente pequeña en el interior del campo vectorial, esta rueda girará, aunque el campo tenga siempre la misma dirección, debido a la diferente magnitud del campo a un lado y a otro de la rueda.

Fuente vectorial y escalar

Al campo vectorial, 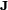\scriptstyle \mathbf{J}, que se obtiene calculando el rotacional de un campo 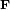\scriptstyle \mathbf{F} en cada punto,

\mathbf{J} = \nabla\times\mathbf{F}

se conoce como las fuentes vectoriales de 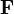\mathbf{F} (siendo las fuentes escalares las que se obtienen mediante la divergencia).

Un campo cuyo rotacional es nulo en todos los puntos del espacio se denomina irrotacional o se dice que carece de fuentes vectoriales. Y si está definido sobre un dominio simplemente conexo entonces dicho campo puede expresarse como el gradiente de una función escalar:

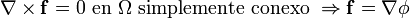
\nabla\times\mathbf{f} = 0\ \mbox{en}\ \Omega\ \mbox{simplemente conexo}\ \Rightarrow \mathbf{f} = \nabla\phi

Expresión en coordenadas cartesianas

Partiendo de la definición mediante un límite, puede demostrarse que la expresión, en coordenadas cartesianas, del rotacional es

\nabla\times \vec F =\left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right)\hat x + \left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right)\hat y + \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right)\hat z

que se puede expresar de forma más concisa con ayuda del operador nabla como un producto vectorial, calculable mediante un determinante:

\nabla\times \vec F=\left| \begin{matrix} \hat x & \hat y & \hat z \\ & & \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ & & \\ F_x & F_y & F_z \end{matrix}\right|

En la notación de Einstein, con el símbolo de Levi-Civita se escribe como:

(\nabla \times \vec F)_k = \epsilon_{klm} \partial_l F_m

Expresión en otros sistemas de coordenadas

Si se emplean sistemas de coordenadas diferentes del cartesiano, la expresión debe generalizarse, para incluir el que los vectores de la base dependen de la posición. Para un sistema de coordenadas ortogonales, como las cartesianas, las cilíndricas o las esféricas, la expresión general precisa de los factores de escala:

\nabla\times \vec F=\frac{1}{h_1h_2h_3}\left| \begin{matrix} h_1\hat{q}_1 & h_2\hat{q}_2 & h_3\hat{q}_3 \\ & & \\ \frac{\partial}{\partial q_1} & \frac{\partial}{\partial q_2} & \frac{\partial}{\partial q_3} \\ & & \\ h_1F_1 & h_2F_2 & h_3F_3 \end{matrix}\right|

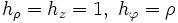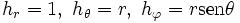(donde, en cartesianas, hx = hy = hz = 1 y reobtenemos la expresión anterior. En coordenadas cilíndricas h_\rho=h_z=1,\ h_\varphi=\rho y en coordenadas esféricas h_r=1,\ h_\theta=r,\ h_\varphi=r {\rm sen}\theta).

Expresión mediante formas diferenciales

Usando la derivada exterior, el rotacional se escribe simplemente como:

dF\,

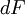
Obsérvese que tomando la derivada exterior de un campo (co)vectorial no da lugar a otro campo vectorial, sino a una 2-forma o un campo de bivector, escrito correctamente como 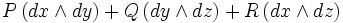P\,(dx \wedge dy) + Q\,(dy \wedge dz) + R\,(dx \wedge dz). Sin embargo, puesto que los bivectores generalmente se consideran menos intuitivos que los vectores ordinarios, el R³-dual se utiliza comúnmente en lugar de otro: esto es una operación quiral, produciendo un pseudovector que adquiere valores opuestos en conjuntos coordenados izquierdos y derechos.

Propiedades

  • Todo campo potencial (expresable como el gradiente de un potencial escalar) es irrotacional y viceversa, esto es,
\vec E = -\nabla \phi\qquad \Leftrightarrow \qquad \nabla\times \vec E =0
  • Todo campo central (radial y dependiente sólo de la distancia al centro) es irrotacional.
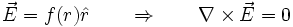
\vec E = f(r) \hat{r}\qquad\Rightarrow \qquad \nabla\times \vec E =0
En particular, el campo eléctrostático de una carga puntual (y por superposición, cualquier campo electrostático) es irrotacional.
  • El rotacional de un campo vectorial es siempre un campo solenoidal, esto es, su divergencia siempre es nula:
\nabla\cdot\left(\nabla\times \vec F\right) \equiv 0

Ejemplos

  • En un tornado los vientos están rotando sobre el ojo, y un campo vectorial que muestra las velocidades del viento tendría un rotacional diferente de cero en el ojo, y posiblemente en otras partes (véase vorticidad).
  • En un campo vectorial que describa las velocidades lineales de cada parte individual de un disco que rota, el rotacional tendrá un valor constante en todas las partes del disco.
  • Si una autopista fuera descrita con un campo vectorial, y los carriles tuvieran diversos límites de velocidad, el rotacional en las fronteras entre los carriles sería diferente de cero.
  • La ley de Faraday de la inducción y la ley de Ampère-Maxwell, dos de las ecuaciones de Maxwell, se pueden expresar muy simplemente usando el rotacional. La primera indica que el rotacional de un campo eléctrico es igual a la tasa de variación de la densidad del flujo magnético, con signo opuesto debido a la Ley de Lenz; la segunda indica que el rotacional de un campo magnético es igual a la suma de la densidad de corrientes y la derivada temporal de la densidad de flujo eléctrico.

Véase también

Obtenido de "Rotacional"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Rotacional — Definición En el cálculo vectorial, el rotacional o rotor es un operador vectorial que muestra la tendencia de un campo vectorial a rotar alrededor de un punto. El que el rotacional de un campo alrededor de un punto sea distinto de cero no… …   Enciclopedia Universal

  • Retraso rotacional — Saltar a navegación, búsqueda En informática, retraso rotacional es un término aplicable a los dispositivos de almacenamiento rotatorios, tales como discos duros, disquetes o las más antiguas memorias de tambor. Se define como el tiempo necesario …   Wikipedia Español

  • Moldeo rotacional — En ingeniería, el moldeo rotacional o rotomoldeo es una técnica de procesamiento de polímeros que permite obtener piezas huecas de tamaño mediano a muy grande con relativamente poco material y buena estabilidad. Contenido 1 Antecedentes… …   Wikipedia Español

  • Modelo vibracional y rotacional nuclear — El modelo vibracional y rotacional para núcleos intenta describir las propiedades de los núcleos atómicos sin recurrir a su estructura interna. Su método es recurrir a unas coordenadas colectivas que describan el movimiento de la “superficie” del …   Wikipedia Español

  • Rotor rígido — Saltar a navegación, búsqueda El rotor rígido es un modelo que se utiliza para explicar el movimiento de los sistemas que rotan. Un rotor rígido es un objeto rígido tridimensional, por ejemplo un trompo o peonza. Para orientar dicho objeto en el… …   Wikipedia Español

  • Ley de Biot-Savart — Ilustración de la ecuación de Biot Savart. La ley de Biot Savart indica el campo magnético creado por corrientes eléctricas estacionarias. En el caso de las corrientes que circulan por circuitos filiformes (o cerrados), la contribución de un… …   Wikipedia Español

  • Campo eléctrico — producido por un conjunto de cargas puntuales. Se muestra en rosa la suma vectorial de los campos de las cargas individuales; . El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacció …   Wikipedia Español

  • Teorema de equipartición — Figura 1. Movimiento térmico de un péptido tipo hélice α. El movimiento vibratorio es aleatorio y complejo, y la energía de un átomo en particular puede fluctuar ampliamente. Sin embargo, el teorema de equipartición permite que se pueda calcular… …   Wikipedia Español

  • Hiperconjugación — En química orgánica, la hiperconjugación es la interacción estabilizante que resulta de la interacción de los electrones en un orbital sigma (generalmente C H o C C) con un orbital pi adyacente vacío, no enlazante o antienlazantes, o con un… …   Wikipedia Español

  • Sobrepastoreo — Sobrepastoreo, causado por la fauna nativa se muestra en la parte superior derecha, Nueva Gales del Sur, Australia …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”