- Wavelet
-
Wavelet
La transformada wavelet o transformada óndula es un tipo especial de transformada de Fourier que representa una señal en términos de versiones trasladadas y dilatadas de una onda finita (denominada óndula madre).
La teoría de óndulas está relacionada con campos muy variados. Todas las transformaciones de óndulas pueden ser consideradas formas de representación en tiempo-frecuencia y, por tanto, están relacionadas con el análisis armónico. Las transformadas de óndulas son un caso particular de filtro de respuesta finita al impulso. Las óndulas, continuas o discretas, como cualquier función L2, responden al principio de incertidumbre de Hilbert (conocido por los físicos como principio de incertidumbre de Heisenberg), el cual establece que producto de las dispersiones obtenidas en el espacio directo y en el de las frecuencias no puede ser más pequeño que una cierta constante geométrica. En el caso de las óndulas discretas, la dispersión de los coeficientes se ha de medir de acuerdo con la norma l2 (norma 2 de series numerables).
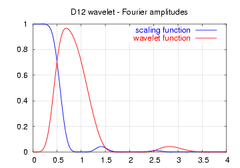
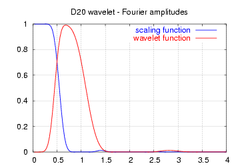
scaling and wavelet functions 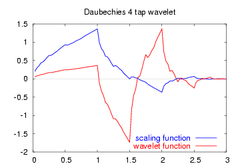
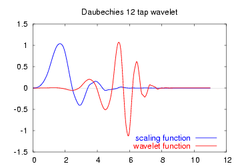
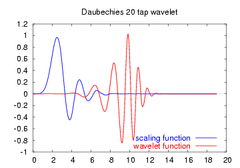
amplitudes of the frequency spectrum 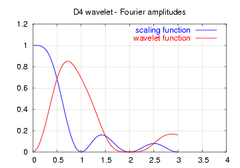
Contenido
Nomenclatura
El término original wavelet, en inglés, ha sido traducido también al castellano como ondículas, ondeletas u onditas. Sin embargo, por su brevedad y mayor semejanza con el paradigma latino, la palabra óndula (un diminutivo culto) es más apropiada para este uso.
Aplicaciones
En cuanto a sus aplicaciones, la transformada de óndula discreta se utiliza para la codificación de señales, mientras la continua se utiliza en el análisis de señales. Como consecuencia, la versión discreta de este tipo de transformada se utiliza fundamentalmente en ingeniería e informática, mientras que la continua se utiliza sobre todo en la física. Este tipo de transformadas están siendo cada vez más empleadas en un amplio campo de especialidades, a menudo sustituyendo a la transformada de Fourier[cita requerida]. Se puede observar este desplazamiento en el paradigma en múltiples ramas de la física, como la dinámica molecular, los cálculos ab initio, la astrofísica, la geofísica de los sismos, la óptica, el estudio de las turbulencias y la mecánica cuántica, así como en otros campos muy variados como el procesamiento digital de imágenes, los análisis de sangre, el análisis de electrocardiogramas, el estudio del ADN, el análisis de proteínas, la meteorología, el procesamiento de señal en general, el reconocimiento de voz, los gráficos por ordenador, el análisis multifractal y en el campo de biometría.
Historia
En términos históricos, el desarrollo de las óndulas entronca con varias líneas de pensamiento, a partir del trabajo de Alfred Haar a principios del siglo XX. Contribuyeron de modo notable al avance de la teoría Goupillaud, Grosman y Morlet con su formulación de lo que hoy conocemos como transformada de óndula continua, Jan Olov-Strömberg con su temprano trabajo sobre óndulas discretas (1983), Ingrid Daubechies, con su propuesta de óndulas ortogonales con soporte compacto (1988), Stephane Mallat y Yves Meyer, con su marco multiresolución (1989), Delrat con su interpretación de la transformada óndulas en tiempo-frecuencia (1991), Newland, con su transformada óndula armónica, y muchos otros desde entonces.
Aplicaciones
- JPEG2000
- DJVU
- Dirac
- SPIHT
Véase también
Enlaces externos
 Wikimedia Commons alberga contenido multimedia sobre Wavelet.Commons
Wikimedia Commons alberga contenido multimedia sobre Wavelet.Commons- Wavelets: ver el bosque y los árboles
- The Wavelet Digest (Inglés)
Categorías: Análisis numérico | Ingeniería electrónica | Procesamiento de señales | Transformaciones | Procesamiento digital de imágenes
Wikimedia foundation. 2010.
