- Ortobicúpula triangular
-
Ortobicúpula triangular 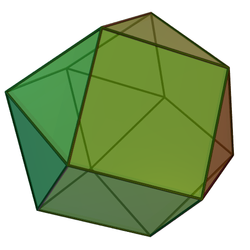
Imágen del sólidoTipo Johnson
J26 - J27 - J28Caras 2+6 triángulos
6 cuadradosAristas 24 Vértices 12 Configuración de los vértices 6(32.42)
6(3.4.3.4)Grupo de simetría D3h Poliedro dual Dodecaedro trapezorrómbico Propiedades convexo En geometría, la ortobicúpula triangular es uno de los sólidos de Johnson (J27). Como sugiere su nombre, puede construirse uniendo dos cúpulas triangulares (J3) por sus bases. Tiene el mismo número de cuadrados y triángulos en cada vértice; sin embargo, no es transitivo por vértices.
La ortobicúpula triangular es la primera ortobicúpula de un conjunto infinito de ellas.
La ortobicúpula triangular tiene cierta similitud con el cuboctaedro, que se llamaría girobicúpula triangular en la nomenclatura de los sólidos de Johnson — la diferencia es que las dos cúpulas triangulares que forman la ortobicúpula triangular están unidas de forma que los triángulos de una de las cúpulas constituyentes tocan triángulos de la otra y los cuadrados tocan otros cuadrados (de ahí el prefijo "orto"); mientras que en el cuboctaedro los triángulos tocan cuadrados y viceversa. Dada una ortobicúpula triangular, al rotar una de las cúpulas 60 grados antes de unir, se forma un cuboctaedro.
La ortobicúpula triangular elongada (J35), que se construye elongando este sólido, tiene una relación especial (diferente) con el rombicuboctaedro.
Los 92 sólidos de Johnson fueron nombrados y descritos por Norman Johnson en 1966.
El dual de la ortobicúpula triangular se llama dodecaedro trapezorrómbico. Tiene 6 caras rómbicas y 6 trapezoidales. Es similar al dodecaedro rómbico y ambos son poliedros que pueden llenar el espacio.
Enlaces externos
Categoría:- Sólidos de Johnson
Wikimedia foundation. 2010.
