- Anticonmutador
-
Anticonmutador
Se define el anticonmutador de dos operadores lineales
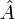y 
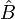como la combinación: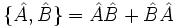
La relación anterior requiere que la intersección de los dominios de ambos operadores sea un conjunto denso de un mismo espacio de Hilbert.
Los anticonmutadores tienen gran importancia en la definición de las álgebras de Clifford, y por tanto, en las relaciones algebraicas que definen los espinores. Una relación que, aunque trivial, es de gran utilidad en los cálculos con operadores lineales no conmutantes es:
![\hat{A}\hat{B} = {1\over2}\Big([\hat{A},\hat{B}] + \{\hat{A},\hat{B}\}\Big)](/pictures/eswiki/98/b9987f32fcfbd4b2b0d141bb2d0b4172.png)
donde
![[\hat{A},\hat{B}]](/pictures/eswiki/99/c081d8bf21108f8283f018b863a75393.png)
es el conmutador de ambos operadores.Aplicaciones
La descripción cuántica de partículas fermiónicas requiere que el anticonmutador los operadores de creación y destrucción cumplan ciertas restricciones.
Véase también
Categoría: Mecánica cuántica
Wikimedia foundation. 2010.
