La paradoja de Russell o paradoja del barbero, descrita por Bertrand Russell en 1901, demuestra que la teoría original de conjuntos formulada por Cantor y Frege es contradictoria.

Contenido 1 La paradoja en términos de conjuntos 2 La paradoja en términos del barbero 3 Explicación de la paradoja 4 Referencias 5 Véase también 6 Enlaces externos

La paradoja en términos de conjuntos

Supongamos un conjunto que consta de elementos que no son miembros de sí mismos. Un ejemplo descrito es el que supone un conjunto que consta de "ideas abstractas". Dicho conjunto es miembro de sí mismo porque el propio conjunto es una idea abstracta, mientras que un conjunto que consta de "libros" no es miembro de sí mismo porque el conjunto en sí no es un libro. Russell preguntaba (en carta escrita a Frege en 1902), si el conjunto de los conjuntos que no forman parte de sí mismos (es decir, aquel conjunto que engloba a todos aquellos conjuntos que no están incluídos en sí mismos, como el de "libros" en el ejemplo anterior) forma parte de sí mismo. La paradoja consiste en que si no forma parte de sí mismo, pertenece al tipo de conjuntos que no forman parte de sí mismos y por lo tanto forma parte de sí mismo. Es decir, formará parte de sí mismo sólo si no forma parte de sí mismo.

Enunciemos la paradoja de otra forma: llamemos M al "conjunto de todos los conjuntos que no se contienen a sí mismos como miembros". Es decir

(1)

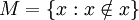
Según la teoría de conjuntos de Cantor, la ecuación (1) se puede representar por

(2)

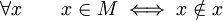
Es decir "Cada conjunto es elemento de M si y sólo si no es elemento de sí mismo". Ahora, en vista de que M es un conjunto, se puede substituir x por M en la ecuación (2), de donde se obtiene

(3)

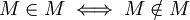
Es decir que M es un elemento de M si y sólo si M no es un elemento de M, lo cual es absurdo.

La paradoja en términos del barbero

La paradoja de Russell ha sido expresada en varios términos más cotidianos, el más conocido es la paradoja del barbero que se puede enunciar de la siguiente manera:

En un lejano poblado de un antiguo emirato había un barbero llamado As-Samet diestro en afeitar cabezas y barbas, maestro en escamondar pies y en poner sanguijuelas. Un día el emir se dio cuenta de la falta de barberos en el emirato, y ordenó que los barberos sólo afeitaran a aquellas personas que no pudieran hacerlo por sí mismas. Cierto día el emir llamó a As-Samet para que lo afeitara y él le contó sus angustias: -- En mi pueblo soy el único barbero. Si me afeito, entonces puedo afeitarme por mí mismo, por lo tanto no debería afeitarme el barbero de mi pueblo ¡que soy yo! Pero, si por el contrario no me afeito, entonces algún barbero me debe afeitar, ¡pero yo soy el único barbero de allí! El emir pensó que sus pensamientos eran tan profundos, que lo premió con la mano de la más virtuosa de sus hijas. Así, el barbero As-Samet vivió para siempre feliz.

En lógica de primer orden, la paradoja del barbero se puede expresar como:

(4)

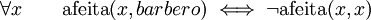
donde afeita(x,y) significa "x es afeitado por y". Lo anterior se leería como "Cada persona es afeitada por el barbero si y sólo si no se afeita a sí misma". Es importante notar la semejanza entre las ecuaciones (2) y (4). Al substituir x por barbero se obtiene

(5)

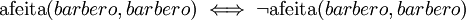
es decir que el barbero se afeita a sí mismo si y sólo si no se afeita a sí mismo, lo cual es una contradicción.

Explicación de la paradoja

Los conjuntos son reuniones de cosas, por ejemplo de coches, libros, personas, etc. y en este sentido los llamaremos conjuntos normales.

La característica principal de un conjunto normal es que no se contiene a sí mismo. Pero también existen conjuntos de conjuntos, como 2^M, que es el conjunto de subconjuntos de M.

Un conjunto de conjuntos es normal salvo si podemos hacerlo que se contenga a sí mismo. Esto último no es difícil si tenemos el conjunto de todas las cosas que NO son libros y como un conjunto no es un libro, el conjunto de todas las cosas que NO son libros formará parte del conjunto de todas las cosas que NO son libros. Estos conjuntos que se contienen a sí mismos se llaman conjuntos singulares.

Está claro que un conjunto dado o bien es normal o bien es singular, no hay término medio, o se contiene a sí mismo o no se contiene. Ahora tomemos el conjunto C como el conjunto de todos los conjuntos normales. ¿Qué clase de conjunto es C? ¿Normal o Singular?

Si es normal, estará dentro del conjunto de conjuntos normales, que es C luego ya no puede ser normal. Si es singular, no puede estar dentro del conjunto de conjuntos normales, luego no puede estar en C, pero si no está en C entonces no es singular.

Cualquier alternativa nos produce una contradicción, ésta es la paradoja.

Referencias

• López Mateos, Manuel (1978). Los Conjuntos. México D.F.: Publicaciones del Departamento de Matemáticas, Facultad de Ciencias, UNAM.

Véase también

• Teoría de conjuntos

Enlaces externos

• Epsilones - Frege y la paradoja de Russell