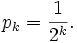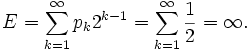Gráfica que muestra el ingreso medio obtenido jugando repetidas veces al juego de la paradoja de San Petesburgo

En teoría de probabilidad y teoría de decisiones, la Paradoja de San Petersburgo es una paradoja que muestra una variable aleatoria cuyo valor es, con una probabilidad alta, muy bajo, pero con un valor esperado infinito. En esta situación, la teoría de decisiones parece recomendar una acción que ninguna persona racional seguiría. Esa apariencia desaparece cuando se tiene en cuenta la utilidad.

La paradoja fue enunciada por Daniel Bernoulli en 1738.

Formulación

Se propone un juego de azar en el que pagas una apuesta inicial fija. Consiste en el lanzamiento de una moneda repetidamente hasta que aparece la primera "cara". Una vez aparece, ganas 1 centavo si la cara aparece en el primer lanzamiento, 2 centavos si aparece en el segundo, 4 centavos si aparece en el tercero, 8 en el cuarto, etc., doblando el premio en cada lanzamiento adicional. Así, ganarías 2^k−1 centavos si la moneda debe lanzarse k veces.

¿Cuánto estarías dispuesto a pagar para jugar a este juego?

Comentario

La probabilidad de que la primera "cara" aparezca en el lanzamiento k es de:

La probabilidad de que ganes más de $10,24 (por ejemplo, 2¹⁰ centavos) es menor que una entre mil. La probabilidad de que ganes más de $1 es menor que una entre cien. A pesar de ello ¡el valor esperado del premio es infinito!

Para calcularlo:

Esta suma diverge a infinito. Así, de acuerdo a la teoría tradicional del valor esperado, no importa cuanto pagues por entrar en el juego, porque saldrás ganando a largo plazo (imagina pagar 1 billón cada vez, para ganar la mayor parte de las veces sólo un par de centavos). Su idea consiste en que las raras ocasiones en las que ganes una cantidad elevada pagarán con creces los cientos de trillones que habrás tenido que pagar para jugar.

Teoría de la utilidad

La idea que sugiere el valor esperado es engañosa. Si se aplica ingenuamente la teoría de decisiones sin tener en cuenta la utilidad, se obtiene que merecería la pena pagar cualquier apuesta inicial.

Se debe considerar además que nadie tiene ni el tiempo ni el dinero necesario para jugar una y otra vez para llegar al largo plazo, o siquiera a una aproximación buena del mismo.

Enlaces externos

• St Petersburg Paradox - Stanford Encyclopaedia of Philosophy (en)

Referencias

• Bernoulli, Daniel: 1738, "Exposition of a New Theory on the Measurement of Risk", Econometrica vol 22 (1954), pp23-36.

Véase también

• Paradojas
• Teoría de juegos
• Probabilidad