Las paradojas de Zenón son una serie de paradojas o aporías, ideadas por Zenón de Elea, para apoyar la doctrina de Parménides de que las sensaciones que obtenemos del mundo son ilusorias, y concretamente, que no existe el movimiento. Racionalmente, una persona no puede recorrer un estadio de longitud, porque primero debe llegar a la mitad de éste, antes a la mitad de la mitad, pero antes aún debería recorrer la mitad de la mitad de la mitad y así eternamente hasta el infinito. De este modo, teóricamente, una persona no puede recorrer un estadio de longitud, aunque los sentidos muestran que sí es posible.

Pertenecen a la categoría de paradojas falsídicas, también llamadas sofismas, esto es, que no sólo alcanzan un resultado que aparenta ser falso, sino que además lo es. Esto se debe a una falacia en el razonamiento, producido por la falta de conocimientos sobre el concepto de infinito en la época en la que fueron formuladas.

Contenido 1 Aquiles y la tortuga 1.1 Réplica a la paradoja 2 La dicotomía 3 La paradoja de la flecha 4 Véase también 5 Referencias

Aquiles y la tortuga

Aquiles, llamado "el de los pies ligeros" y el más hábil guerrero de los Aqueos, quien mató a Héctor, decide salir a competir en una carrera contra una tortuga. Ya que corre mucho más rápido que ella, y seguro de sus posibilidades, le da una gran ventaja inicial. Al darse la salida, Aquiles recorre en poco tiempo la distancia que los separaba inicialmente, pero al llegar allí descubre que la tortuga ya no está, sino que ha avanzado, más lentamente, un pequeño trecho. Sin desanimarse, sigue corriendo, pero al llegar de nuevo donde estaba la tortuga, ésta ha avanzado un poco más. De este modo, Aquiles no ganará la carrera, ya que la tortuga estará siempre por delante de él.

Réplica a la paradoja

Actualmente, se conoce que Aquiles realmente alcanzará a la tortuga,^[1] ya que, como demostró el matemático escocés James Gregory (1638-1675), una suma de infinitos términos puede tener un resultado finito. Los tiempos en los que Aquiles recorre la distancia que lo separa del punto anterior en el que se encontraba la tortuga son cada vez más y más pequeños, y su suma da un resultado finito, que es el momento en que alcanzará a la tortuga.

Otra manera de plantearlo es que Aquiles puede fijar un punto de llegada que está metros delante de la tortuga en vez del punto en que ella se encuentra. Ahora, en vez de cantidades infinitas, tenemos dos cantidades finitas con las cuales se puede calcular un espacio finito de tiempo en el cual Aquiles pasará a la tortuga.

Otra forma de encarar el problema es huyendo del análisis infinitesimal, cuyo planteamiento matemático se desconocía en tal época, para reconvertirlo en análisis discreto: Filípides -el campeón olímpico al que se ordenó que abandonara las filas del ejército para comunicar a Atenas la victoria conseguida sobre los persas en la playa de Marathon- no recorre espacios infinitesimales, sino discretos, que podemos denominar zancada. A cada zancada le podemos asignar un espacio concreto. Por ejemplo podemos suponer que Filípides recorre un metro a cada zancada. Ahora el problema se reduce a la comparación de velocidades relativas: calcular en qué momento la última zancada de Filípides recorrerá una distancia mayor a la que haya podido recorrer la tortuga en el mismo tiempo, incluso aunque no sepamos definir la distancia exacta que la tortuga recorrería. Es decir, basta que una de las variables sea discreta y que podamos suponer que, en determinado tiempo, puede superar a las distancias infinitesimales, para demostrar, incluso teóricamente, que el movimiento existe.

El tema está en que la paradoja sólo se presenta considerando el espacio sin el tiempo, cuando sabemos que el movimiento es una función "continua" del espacio en función del tiempo.

La dicotomía

Esta paradoja, conocida como argumento o paradoja de la dicotomía, es una variante de la anterior.

Zenón está a ocho metros de un árbol. Llegado un momento, lanza una piedra, tratando de dar al árbol. La piedra, para llegar al objetivo, tiene que recorrer antes la primera mitad de la distancia que lo separa de él, es decir, los primeros cuatro metros, y tardará un tiempo (finito) en hacerlo. Una vez llegue a estar a cuatro metros del árbol, deberá recorrer los cuatro metros que le quedan, y para ello debe recorrer primero la mitad de esa distancia. Pero cuando esté a dos metros del árbol, tardará tiempo en recorrer el primer metro, y luego el primer medio metro restante, y luego el primer cuarto de metro... De este modo, la piedra nunca llegará al árbol.

Es posible utilizar este razonamiento, de forma análoga, para «demostrar» que la piedra nunca llegará a salir de la mano de Zenón.

Al igual que en la paradoja de Aquiles y la tortuga, es cierto que el número de puntos recorridos (y tiempos invertidos en hacerlo, según el argumento de la paradoja) es infinito, pero su suma es finita y por tanto la piedra llegará al árbol.

La paradoja de la piedra puede ser planteada matemáticamente usando series infinitas. Las series infinitas son sumas cuyo término variante (que puede tomar cualquier valor numérico) va hasta el infinito. Las series infinitas pueden ser convergentes o divergentes, en el primer caso la suma de las mismas es un número finito, en el segundo no.

Como introducción al concepto de serie, se muestran un par de series sencillas y luego se aplica esa formulación a la paradoja de Zenón.

Para sumar todos los números desde 1 a infinito

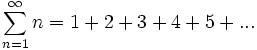
Para sumar todos los números al cuadrado desde 1 a infinito

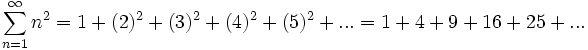
Para plantear una serie que modele la paradoja de la piedra se hace una serie que sume la mitad, luego la mitad de la mitad, luego la mitad de la mitad de la mitad y así, hasta el infinito

La serie que se plantea es una serie geométrica, por lo que su suma puede ser calculada con la siguiente fórmula:

Suma =

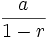
En el sumatorio de la paradoja de Zenón, «a» es y «r» es la razón de incremento (producto), que es . Sustituyendo esos valores en la fórmula de suma se tiene:

Suma =

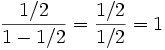
Entonces se tiene que la suma de la mitad de «algo» más la mitad de la mitad de «algo» y así sucesivamente da 1, «algo» completo. Esto también es aplicable a la paradoja, la mitad de la distancia, más la mitad de la mitad de la distancia y así sucesivamente da como resultado la distancia entera. Por lo tanto se concluye que, recorriendo infinitas mitades es posible recorrer toda la distancia.

La paradoja de la flecha

En esta paradoja, se lanza una flecha. En cada momento en el tiempo, la flecha está en una posición específica, y si ese momento es lo suficientemente pequeño, la flecha no tiene tiempo para moverse, por lo que está en el reposo durante ese instante. Ahora bien, durante los siguientes periodos de tiempo, la flecha también estará en reposo por el mismo motivo. De modo que la flecha está siempre en reposo: el movimiento es imposible.

Un modo de resolverlo es observar que, a pesar de que en cada instante la flecha se percibe como en reposo, estar en reposo es un término relativo. No se puede juzgar, observando sólo un instante cualquiera, si un objeto está en reposo. En lugar de ello, es necesario compararlo con otros instantes adyacentes. Así, si lo comparamos con otros instantes, la flecha está en distinta posición de la que estaba antes y en la que estará después. Por tanto, la flecha se está moviendo.

Otra perspectiva es acudir, directamente, a la definición de velocidad, cuya idea esencial es la de cambio: se cambia de espacio en un tiempo determinado. Así que, por definición, un cuerpo que se mueve, sin alterar el volumen de espacio que ocupa en cada momento, cambia de espacio, es decir, ocupa la misma cantidad, volumen, y forma de espacio, pero en un lugar distinto, al momento siguiente. El movimiento sería la sucesión de los distintos espacios ocupados por el cuerpo (móvil) en la sucesión de los distintos momentos que componen la magnitud de tiempo considerada. Así, si asumimos que el concepto velocidad, es decir, movimiento, puede definirse racionalmente, simultáneamente estamos admitiendo que el movimiento, racionalmente, en teoría, existe.

Véase también

• Aporía

Referencias