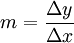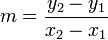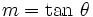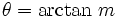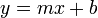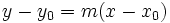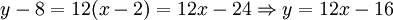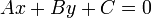Pendiente de la recta

Pendiente de la recta

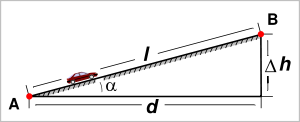Pendiente de la recta

Para otros usos de este término, véase Pendiente.
Pendiente de una carretera.

En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento ideal, natural o constructivo respecto de la horizontal (la tangente del valor de la "m" es el ángulo en radianes).

Puede referirse a la pendiente de una recta, caso particular de la tangente a una curva cualquiera, en cuyo caso representa la derivada de la función en el punto considerado, y es un parámetro relevante en el trazado altimétrico de carreteras, vías férreas, canales y otros elementos constructivos.

Contenido

Definición de la pendiente

La pendiente de una recta en un sistema de representación triangular (cartesiano ), suele ser representado por la letra m, y es definido como el cambio o diferencia en el eje Y dividido por el respectivo cambio en el eje X, entre 2 puntos de la recta. En la siguiente ecuación se describe:

m = \frac{\Delta y}{\Delta x}

(El símbolo delta "Δ", es comúnmente usado en calculo para representar un cambio o diferencia).

Dados dos puntos (x1,y1) y (x2,y2), la diferencia en X es x2 − x1, mientras que el cambio en Y se calcula como y2 − y1. Sustituyendo ambas cantidades en la ecuación descrita anteriormente obtenemos:

m = \frac{y_2 - y_1}{x_2 - x_1}

que no encontramos que es pendiente entre dos puntos

Geometría

Mientras el valor de la pendiente sea mayor, la recta tendrá a su vez mayor inclinación. Una línea horizontal tiene pendiente = 0, mientras que una que forme un ángulo de 45° con el eje X tiene una pendiente = +1 (si la recta "sube hacia la derecha"). Una recta con 45° de inclinación que "baje hacia la derecha", tiene pendiente = -1. Una recta vertical no tiene un número real que la defina, ya que su pendiente tiende a infinito.

El ángulo θ que una recta tiene con el eje positivo de X, está relacionado con la pendiente M, en la siguiente ecuación:

m = \tan\,\theta

y

\theta = \arctan\,m

(ver Trigonometría).

Dos o más rectas son paralelas si ambas poseen la misma pendiente, o si ambas son verticales y por ende no tienen pendiente definida; 2 o más rectas son perpendiculares (forman un ángulo recto entre ellas), si el producto de sus pendientes es igual a -1, o una posee pendiente 0 y la otra no esta definida (infinita).

La pendiente en las ecuaciones de la recta

Si y es una función lineal de x, entonces el coeficiente de x es la pendiente de la recta. Por lo tanto, si la ecuación está dada de la siguiente manera:

y = mx + b \,

entonces m es la pendiente. En esta ecuación, el valor de b puede ser interpretado como el punto donde la recta intersecta al eje Y, es decir, el valor de y cuando x = 0. Este valor también es llamado ordenada al origen.

Si la pendiente m de una recta y el punto (x0,y0) de la recta son conocidos, entonces la ecuación de la recta puede ser encontrada usando:

y - y_0 = m(x - x_0) \,

Por ejemplo, considere una recta que pasa por los puntos (2, 8) y (3, 20). Esta recta tiene pendiente 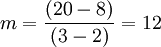m = \frac{(20 - 8)}{(3 - 2)} = 12. Luego de esto, uno puede definir la ecuación para esta recta usando la fórmula antes mencionada:

y - 8 = 12(x - 2) = 12x - 24 \Rightarrow y = 12x - 16


La pendiente de la recta en la fórmula general:

Ax + By + C = 0 \,

está dada por: -\frac{A}{B}

Véase también

  • Derivada
  • Gradiente
  • Lista de pendientes y deformaciones en vigas
  • Trazado altimétrico
Obtenido de "Pendiente de la recta"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Pendiente de una recta — La pendiente de una recta es el cociente entre un diferencia de ordenadas y la correspondiente diferencia de abscisas , siendo y puntos de la recta …   Enciclopedia Universal

  • Recta de balance — Saltar a navegación, búsqueda En microeconomía, se entiende por recta de balance o restricción presupuestaria, al conjunto de distintas cantidades de dos bienes que pueden ser consumidas por un individuo, partiendo de una determinada renta o… …   Wikipedia Español

  • Recta — Para otros usos de este término, véase Recta (desambiguación). Se ha sugerido que Línea sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí …   Wikipedia Español

  • Pendiente — ► adjetivo 1 Que pende o cuelga. SINÓNIMO colgante 2 Que está inclinado respecto de un plano. SINÓNIMO oblicuo 3 Se aplica a los asuntos u otras cosas que están por resolver: ■ la causa está pendiente de sentencia. 4 Se refiere a la persona que… …   Enciclopedia Universal

  • Recta tangente — Saltar a navegación, búsqueda Sea C una curva, y A un punto de esta. Se supone que A es un punto regular de la curva, es decir que no es un punto anguloso: La curva no cambia repentinamente de dirección en A. La tangente a C en A es la recta TA… …   Wikipedia Español

  • pendiente — (Del ant. part. act. de pender; lat. pendens, entis). 1. adj. Que pende. 2. Inclinado, en declive. Terreno pendiente. 3. Que está por resolverse o terminarse. 4. Sumamente atento, preocupado por algo que se espera o sucede. Todos estaban… …   Diccionario de la lengua española

  • Recta — ► sustantivo femenino 1 GEOMETRÍA Línea que une dos puntos. 2 Parte de una carretera o de un circuito trazados como esta línea. FRASEOLOGÍA recta de llegada DEPORTES La última antes de llegar a la meta, en algunos deportes. * * * recta f. Línea… …   Enciclopedia Universal

  • hilera recta — ► locución CONSTRUCCIÓN La de adoquines dispuesta en mitad de la calzada, a partir de la cual el pavimento se halla dispuesto en pendiente transversalmente hasta la acera …   Enciclopedia Universal

  • Derivada — La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en negro; la tangente a la curva está dibujada en rojo). En matemáticas, la derivada de una función es una medida… …   Wikipedia Español

  • Función polinómica de grado 1 — Saltar a navegación, búsqueda Un polinomio de primer grado de una variable real es una función matemática de la forma: donde m y b son constantes. Una función lineal de una única variable independiente x suele escribirse en la forma siguiente …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”