- Postulados de Golomb
-
Postulados de Golomb
Los postulados de Golomb son condiciones necesarias pero no suficientes para que secuencias seudoaleatorias parezcan ser aleatorias, enunciados por el ingeniero y matemático estadounidense Solomon W. Golomb.
Sea s=s0,s1,s2,..... una secuencia de período N, los postulados plantean que:
- En el ciclo sn de s, la cantidad de '1' difiere de la cantidad de '0' como máximo en 1.
- En el ciclo sn, al menos la mitad de las rachas tienen longitud 1, al menos la cuarta parte, longitud 2, al menos un octavo longitud 3, etc. Además para cada una de esas rachas hay la misma cantidad de huecos y de bloques.
- La función de autocorrelación tiene sólo 2 valores racionales:
-
- C(t)=1 (si t=0) y c(t)=K/N; donde K
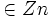 para
para 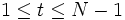
- C(t)=1 (si t=0) y c(t)=K/N; donde K
Qué es hueco y bloque
1000001 hueco de 5 (mide 0 consecutivos)
0111110 bloque de 5 (mide 1 consecutivos)
Una secuencia que cumple con los postulados de Golomb se llaman pn-secuencia
Véase también
Categoría: Generadores de números pseudoaleatorios
Wikimedia foundation. 2010.
