Los postulados de Euclides, hace referencia al tratado denominado Los Elementos, escrito por Euclides hacia el año 300 a. C., exponiendo los conocimientos geométricos de la Grecia clásica deduciéndolos a partir de cinco postulados, considerados los más evidentes y sencillos; estos son:^[1]

Representación geométrica de los postulados de Euclides.

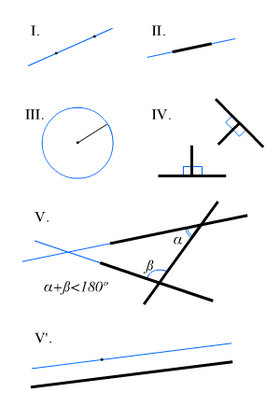
1. Por dos puntos diferentes sólo se puede trazar una línea recta.
2. Todo segmento rectilíneo se puede prolongar indefinidamente.
3. Con un centro y un radio dado sólo se puede trazar una circunferencia.
4. Todos los ángulos rectos son iguales.
5. Si una recta corta a otras dos formando a un lado ángulos internos, y la suma de estos es menor que dos rectos, las dos rectas prolongadas indefinidamente se encontrarán de ese lado.

El primer postulado lo emplea Euclides, no sólo en el sentido de que por dos puntos pasa una recta, sino de que ésta es única, porque tal unicidad era el noveno de sus axiomas. Es verosímil que este axioma esté intercalado, y algunos consideran que debe colocarse entre los postulados, complementando al primero. El cuarto postulado, que pudiera parecer algo oscuro a una mentalidad moderna, es utilizado por Euclides en el sentido de que cualquier ángulo recto puede superponerse sobre cualquier otro.

Terminología actual

En términos actuales, estos postulados podrían entenderse así: el primero y el tercero, al afirmar la posibilidad de trazar rectas y círculos, apuntan directamente a la estructura subyacente. Hoy en día, la estructura más natural que hace posibles los conceptos de distancia y curva con dirección constante es la de geometría riemanniana.

El cuarto postulado afirma que el grupo de las isometrías de la superficie actúa transitivamente en los puntos y los vectores de módulo 1; es decir, dado un vector e de módulo 1 en un punto p y otro vector v de módulo 1 en otro punto q, existe alguna isometría de la superficie que transforma p en q y e en v. Es posible demostrar que las únicas superficies riemannianas que satisfacen tal condición son el plano euclídeo, el plano hiperbólico, el plano proyectivo y la esfera.

Si exigimos que por dos puntos pase una única línea recta, excluimos la geometría esférica, porque por dos puntos diametralmente opuestos (el polo norte y el polo sur) pasan infinitos meridianos (que son las líneas en la esfera).

Si, con el segundo postulado, imponemos que las rectas tengan longitud infinita, eliminamos el plano proyectivo, porque todas sus rectas tienen longitud finita (más aún, son compactas porque el plano proyectivo lo es). Sólo el plano euclídeo y el plano hiperbólico satisfacen los cuatro primeros postulados. Ahora el quinto postulado deja como única posibilidad el plano euclídeo, que es precisamente la estructura desentrañada por la geometría griega.

Vemos así claramente que, cuando a principios del siglo XIX Gauss, Lobachevsky y János Bolyai consideraron la posibilidad de una geometría sin el quinto postulado, descubrieron necesariamente la Geometría hiperbólica. Ésta fue la primera geometría no euclídea en aparecer históricamente y Gauss consideró seriamente la posibilidad de que fuera la geometría del espacio en que vivimos, planteando así la cuestión de la estructura geométrica del Universo, que conduciría a la Teoría de la relatividad general de Einstein. Gauss incluso llegó a presentir que la geometría hiperbólica era preferible, porque en ella hay unidades de longitud naturales.

Referencias

Enlaces externos

• Los Elementos de Euclides.