En matemática, una presentación es una forma de definir un grupo mediante la especificación de dos conjuntos:

• S, conjunto de los generadores, de modo que todo elemento del grupo pueda expresarse como producto de elementos de S.
• R, conjunto de las relaciones, igualdades entre elementos del grupo.

La presentación de un grupo G suele escribirse en la forma 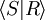. En las relaciones en que el segundo miembro de la igualdad sea el elemento neutro del grupo, suele omitirse la igualdad y el elemento neutro. Por ejemplo:

G = < a,b,c,d | b⁹,cbcbcb,cbc ^{− 1}b ^{− 1} >

indica que el grupo G está generado por a, b, c, d ; y el conjunto de relaciones nos indica que b⁹= e, es decir, b es de orden 9, cb es de orden 3, y que c y b conmutan.

Introducción informal

Llamamos palabra a cualquier producto de elementos del grupo o de sus inversos. Por ejemplo, si x, y, z son elementos de un grupo G, entonces xy, z^-1xzz son palabras en el conjunto {x, y, z}.

Diremos que un grupo G está generado por un conjunto S, si es posible describir todo elemento de G como producto de la forma

x₁^a₁ x₂^a₂ ... x_n^a_n

donde todos los x_i son elementos de S, y cada a_i es un número entero. Es decir, si todo elemento de G puede expresarse como una palabra en S.

Si G no es un grupo libre, muchos de estos productos serán iguales. Será necesario precisar todas estas relaciones a partir de un conjunto R de relaciones básicas de las que se deduzcan las demás,

Definición

Decimos que un grupo G tiene una presentación 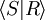donde S especifica los objetos (o símbolos) -usualmente letras- que generan a todos los elementos del grupo, esto es, todo elemento del grupo se escribe como una palabra de elementos en S y R las relaciones (palabras) básicas que determinan el carácter especial del grupo.

Informalmente la presentación 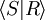es la más libre posible si S está sujeto a R. Formalmente G tiene la presentación dada si G es el cociente del grupo libre generado por S entre el subgrupo normal generado por las relaciones R, i.e. la clausura normal de R.

Ejemplos

1. Un grupo cíclico de orden n tiene un solo generador, y una presentación 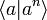. Este grupo es isomorfo a .
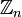2. Los números enteros 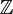tienen una presentación 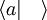donde el conjunto de relaciones es vacío, de hecho este grupo coincide con un grupo libre de un solo generador.
3. Otro ejemplo más complejo es la presentación 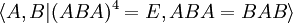, que determina un grupo que es isomorfo a 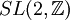un ejemplo de grupo especial general.

Producto libre y producto directo

Si G tiene una presentación <S|R> y H una presentación <T|Q> con S y T disjuntos, entonces el producto libre G * H tiene una presentación <S,T|R,Q>.

Si G tiene una presentación <S|R> y H una presentación <T|Q> con S y T disjuntos, entonces el producto directo de G y H tiene una presentación <S,T|R,Q, [S,T]>. aquí, [S,T] representa las relaciones necesarias para que todo elemento de S conmute con todo elemento de T.