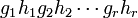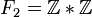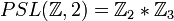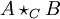Producto libre de grupos

Producto libre de grupos

Producto libre de grupos

En las matemáticas, particularmente en la teoría de grupos, el producto libre de grupos es la construcción de un nuevo grupo a partir de una dada colección de ellos y que permite la inclusión como subgrupos a cada uno de los factores que le construyen.

Para ilustrar la construcción, más precisamente, utilicemos dos grupos G, H. Entonces su producto libre es el grupo G * H que consiste en un nuevo grupo cuyos elementos tienen la forma canónica

g_1h_1g_2h_2\cdots g_rh_r

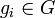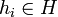donde los g_i\in G y los h_i\in H es decir los elementos de G*H son palabras reducidas de letras alternadas que son elementos de los dos grupos G y H respectivamente.

Entonces uno puede pensar que el grupo G está incluido en G*H pues trivialmente vemos que cada elemento de G es una palabra reducida en G*H, y similarmente para H.

Un ejemplo básico es el grupo libre, F2 de rango dos; éste, se puede interpretar como

F_2=\mathbb{Z}*\mathbb{Z}

Otro un poco más complejo es 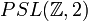PSL(\mathbb{Z},2) que se interpreta como

PSL(\mathbb{Z},2)=\mathbb{Z}_2*\mathbb{Z}_3

Generalizaciones

Una manera similar pero más general de construir grupos a partir de antiguos es el producto libre amalgamado, que consiste empezar con dos grupos arbitrarios A, B y un tercer C que se encuentra encajado es ambos A y B, entonces uno toma el cociente 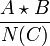\frac{A\star B}{N(C)}\, a partir del producto libre de A con B y haciendo módulo N(C) que es la clausura normal de C en ambos A, B.

En símbolos matemáticos se acostumbra a escribir al producto libre de A con B amalgamados por C como:

A\star_{C}B

Ejemplos de esta construcción aparecen en el teorema de Seifert-van Kampen donde se calcula es grupo fundamental de un espacio topológico en términos de los grupos fundamentales de algunos de sus subespacios.

Referencias

  1. libro de Ross Geoghegan: Topological methods in group theory, GTM-243 (2008), Springer ISBN 978-0-387-74611-1.
  2. panfleto de Peter Scott y Terry Wall titulado: Topological methods in group theory, London Math. Soc. Lecture Note Ser., 36, Cambridge Univ. Press (1979) 137-203. En dirección [1], en el apartado de sources for the Bass Serre theory puedes descargarlo.
Obtenido de "Producto libre de grupos"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Producto tensorial — Saltar a navegación, búsqueda En matemáticas, el producto tensorial, denotado por , se puede aplicar en diversos contextos a vectores, matrices, tensores y espacios vectoriales. En cada caso la significación del símbolo es la misma: la operación… …   Wikipedia Español

  • Grafo de grupos — En teoría geométrica de grupos, un grafo de grupos es un objeto que consiste en una colección de grupos indexados por los vértices y arista de un grafo, junto con una familia de monomorfismos de los grupos de aristas en los grupos de vértices.… …   Wikipedia Español

  • Software libre — Mapa conceptual del software libre. El software libre (en inglés free software, aunque esta denominación también se confunde a veces con gratis por la ambigüedad del término free en el idioma inglés, por lo que también se usa libre software y… …   Wikipedia Español

  • Tratado de Libre Comercio entre Estados Unidos — Tratado de Libre Comercio entre Estados Unidos, Centroamérica y República Dominicana Saltar a navegación, búsqueda «CAFTA» redirige aquí. Para otras acepciones, véase CAFTA (desambiguación) …   Wikipedia Español

  • Hardware libre — |añoacceso=2009 |autor= |enlaceautor= |idioma= }}</ref>]] Hardware libre de Bug Labs.[1] …   Wikipedia Español

  • Tratado de Libre Comercio entre Estados Unidos, Centroamérica y República Dominicana — «CAFTA» redirige aquí. Para otras acepciones, véase CAFTA (desambiguación). El área CAFTA está formada por los países de …   Wikipedia Español

  • Anexo:Grupos finitos de orden bajo — Este artículo muestra una lista matemática de los grupos finitos de orden bajo (una cardinalidad de hasta 16 elementos) clasificados por isomorfismo de grupos. Con esta lista se puede determinar de qué grupo conocido es isomorfo un grupo finito G …   Wikipedia Español

  • Historia del software libre y de código abierto — Mapa conceptual del software libre. La historia del software libre y de código abierto como lo conocemos actualmente, se remonta a inicios de los años 1980, época en la que la mayoría de software era privativo y surgió la necesidad, por parte de… …   Wikipedia Español

  • Mercado libre — Para otros usos de este término, véase Mercado libre (desambiguación). Se puede definir el mercado libre como el sistema en el que el precio de los bienes o servicios es acordado por el consentimiento entre los vendedores y los consumidores,… …   Wikipedia Español

  • Grupo libre — grafo de Cayley del grupo libre de dos generadores, a y b. En teoría de grupos, un grupo G se dice libre si hay un subconjunto S de G, tal que todo elemento de G puede escribirse en una forma única como producto de finitos elementos de S y sus… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”