Problema de Plateau

Problema de Plateau

Problema de Plateau

Problema de Plateau

Se dan dos puntos P1(x1,y1) y P2(x2,y2) del plano xy. Sea 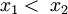x_1<\;x_2. Supongamos que y = y(x) es la ecuación de una curva que une los puntos P1 y P2, es decir,

y = y(x1), y = y(x2).

La curva gira alrededor del eje x barriendo cierta superficie de revolución. Se pregunta: ¿cuál es la superficie de rotación que tiene la menor área posible? De este modo se llega al problema de la elección de la función y(x) para la que la integral

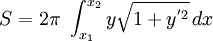
S=2\pi\ \int_{x_1}^{x_2} y \sqrt{1+y^{'2}}\, dx

(área de la superficie de revolución) es mínima. Estas superficies de revolución mínimas, bajo ciertas restricciones adicionales sobre los puntos P1 y P2, se denominan catenoides.

La generalización del problema formulado consiste en lo siguiente:

Se da una curva cerrada (de Jordan) en el espacio. Hallar la superficie que contiene esta curva y tal que el área abarcada por la curva sea mínima.

Éste es el problema que se conoce como problema de Plateau.

Enlaces externos

Obtenido de "Problema de Plateau"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Joseph-Antoine Ferdinand Plateau — Joseph Antoine Ferdinand Plateau. Daguerrotipo fechado en 1843. Joseph Antoine Ferdinand Plateau (Bruselas, Bélgica, 14 de octubre de 1801 – Gante, Bélgica, 15 de septiembre de 1883) fue un físico belga que definió en 1829 el principio de la… …   Wikipedia Español

  • Pompa de jabón — Saltar a navegación, búsqueda Burbuja redirige aquí. Para el término de economía, véase Burbuja económica …   Wikipedia Español

  • Jesse Douglas — (3 de julio de 1897 – 7 de octubre de 1965) fue un matemático estadounidense. Nació en Nueva York y asistió a la Universidad de Columbia entre 1920 y 1924. Fue uno de los ganadores de la primera entrega de la Medalla Fields, otorgada en 1936. Se… …   Wikipedia Español

  • Anatoli Fomenko — Saltar a navegación, búsqueda Anatoli Timoféyevich Fomenko (Анатолий Тимофеевич Фоменко). Matemático ruso. Nació en Donetsk (Ucrania) el 13 de marzo de 1945. Es miembro numerario de la Academia de Ciencias de Rusia (ACR) Desde 1969 trabajó en el… …   Wikipedia Español

  • Jim Simons — Simons en 2007, en la Conferencia Differential Geometry, Mathematical Physics, Mathematics and Society en Bures sur Yvette …   Wikipedia Español

  • Bicyclette Brompton — Brompton Bicycle Logo de Brompton Bicycle Création 03 06 1976 Fondateur(s) Andrew Ritchie …   Wikipédia en Français

  • Brompton Bicycle — 51° 29′ 27″ N 0° 17′ 35″ W / 51.4907, 0.2931 …   Wikipédia en Français

  • Brompton bicycle — Logo de Brompton Bicycle Création 03 06 1976 Fondateur(s) Andrew Ritchie …   Wikipédia en Français

  • Estructura de Weaire-Phelan — Saltar a navegación, búsqueda La estructura de Weaire Phelan es una estructura tridimensional compleja. En 1993, Denis Weaire y Robert Phelan, dos físicos del Trinity College (Dublín), descubrieron que, en simulaciones informáticas de la espuma,… …   Wikipedia Español

  • Kentucky — Mancomunidad de Kentucky Commonwealth of Kentucky Estado de los Estados Unidos …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”