- Problema del caballo
-
Problema del caballo
El Problema del caballo es un antiguo problema matemático en el que se pide que, teniendo una cuadrícula de n x n casillas y un caballo de ajedrez colocado en una posición cualquiera ( x, y ), el caballo pase por todas las casillas y una sola vez. Lo que resulta en n2-1 movimientos.
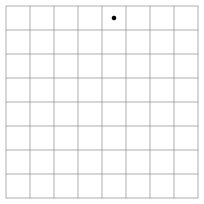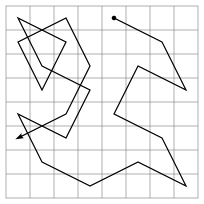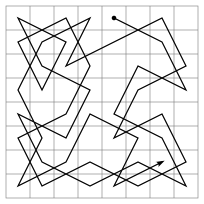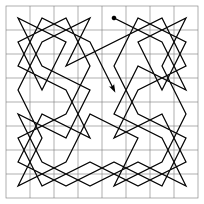Solución para 63 saltos de caballo por las 64 casillas.
Muchos matemáticos han buscado una solución matemática a este problema, entre ellos Euler.
Se han encontrado muchas soluciones a este problema y de hecho no se sabe con seguridad de cuántas maneras diferentes es posible solucionarlo.
Algunas variaciones de este problema han sido estudiadas por los matemáticos, tales como:
- Buscar soluciones cíclicas, en la cual se debe llegar a la misma casilla de la cual se partió.
- Tableros de diferente número de columnas o diferente número de filas.
- Juegos de dos jugadores basados en la idea.
- Problemas usando ligeras variaciones en la forma de moverse el caballo.
El problema del caballo es una forma del problema más general Problema de la ruta Hamiltoniana en la teoría de grafos.
A la derecha podemos apreciar una de las posibles soluciones en un tablero de ajedrez convencional de ocho columnas por ocho filas. Abajo, una solución cíclica en que la casilla de destino es justo la anterior a la de partida.
63 14 37 24 51 26 35 10 22 39 62 13 36 11 50 27 15 64 23 38 25 52 9 34 40 21 16 61 12 33 28 49 17 60 1 44 29 48 53 8 2 41 20 57 6 55 32 47 59 18 43 4 45 30 7 54 42 3 58 19 56 5 46 31 
Otra solución del matemático Euler.El problema del caballo en la literatura
La novela La vida: Instrucciones de uso, de Georges Perec, está construida según un esquema del "problema del caballo": A la trama de casillas del tablero corresponden las diferentes ventanas de una fachada. La narración, por tanto, se construyó como un procedimiento de combinatoria de los elementos literarios situados en cada una de las casillas.
Véase también
Enlaces externos
- Código libre en Python (en español)
- The knight's tour (en inglés)
- Knight's tour notes (en inglés)
Categorías: Problemas de ajedrez | Problemas matemáticos | Problemas computacionales | Teoría de grafos
Wikimedia foundation. 2010.
