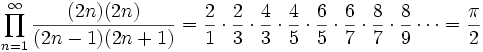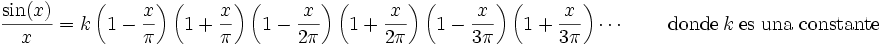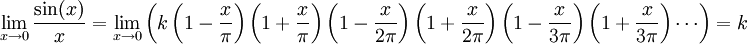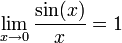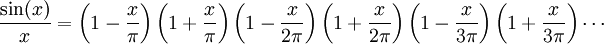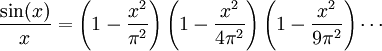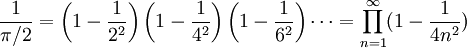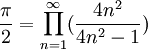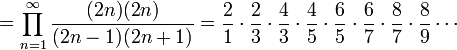Producto de Wallis

Producto de Wallis

Producto de Wallis

En matemáticas, se conoce como Producto de Wallis una expresión utilizada para representar el valor de π que fue descubierta por John Wallis en 1655 y que establece que:


\prod_{n=1}^{\infty} \frac{(2n)(2n)}{(2n-1)(2n+1)} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}

Demostración

Antes que nada se debe considerar que la raíz de sin(x)/x es ±nπ, donde n = 1, 2, 3,... Entonces, podemos expresar el seno como un producto infinito de factores lineales de sus raíces:

\frac{\sin(x)}{x} = k \left(1 - \frac{x}{\pi}\right)\left(1 + \frac{x}{\pi}\right)\left(1 - \frac{x}{2\pi}\right)\left(1 + \frac{x}{2\pi}\right)\left(1 - \frac{x}{3\pi}\right)\left(1 + \frac{x}{3\pi}\right) \cdots \qquad\ \textrm{donde}~k~\textrm{es~una~constante}

Para encontrar la constante k, se toma el límite en ambos lados:

\lim_{x \to 0} \frac{\sin(x)}{x} = \lim_{x \to 0} \left( k \left(1 - \frac{x}{\pi}\right)\left(1 + \frac{x}{\pi}\right)\left(1 - \frac{x}{2\pi}\right)\left(1 + \frac{x}{2\pi}\right)\left(1 - \frac{x}{3\pi}\right)\left(1 + \frac{x}{3\pi}\right) \cdots \right) = k

Sabiendo que:

\lim_{x \to 0} \frac{\sin(x)}{x} = 1

Hacemos k=1. Obtenemos la fórmula de Euler-Wallis para el seno:

\frac{\sin(x)}{x} = \left(1 - \frac{x}{\pi}\right)\left(1 + \frac{x}{\pi}\right)\left(1 - \frac{x}{2\pi}\right)\left(1 + \frac{x}{2\pi}\right)\left(1 - \frac{x}{3\pi}\right)\left(1 + \frac{x}{3\pi}\right) \cdots
\frac{\sin(x)}{x} = \left(1 - \frac{x^2}{\pi^2}\right)\left(1 - \frac{x^2}{4\pi^2}\right)\left(1 - \frac{x^2}{9\pi^2}\right) \cdots

Haciendo x=π/2, se obtiene:

\frac{1}{\pi / 2} = \left(1 - \frac{1}{2^2}\right)\left(1 - \frac{1}{4^2}\right)\left(1 - \frac{1}{6^2}\right) \cdots = \prod_{n=1}^{\infty} (1 - \frac{1}{4n^2})
\frac{\pi}{2} = \prod_{n=1}^{\infty} (\frac{4n^2}{4n^2 - 1})
= \prod_{n=1}^{\infty} \frac{(2n)(2n)}{(2n-1)(2n+1)} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots

Q.E.D.

Enlaces externos

Obtenido de "Producto de Wallis"

Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Wallis y Futuna — No debe confundirse con Islas Willis. Uvea mo Futuna Territoire des Îles Wallis et Futuna Colectividad de ultramar de Francia …   Wikipedia Español

  • John Wallis — John Wallis. John Wallis (Ashford, 23 de noviembre de 1616 – Oxford, 28 de octubre de 1703) fue un matemático inglés a quien se atribuye en parte el desarrollo del cálculo moderno. Fue un precursor del cálculo infinitesi …   Wikipedia Español

  • Número π — π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El… …   Wikipedia Español

  • Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención …   Wikipedia Español

  • Mata-Utu — Matā utu Mata Utu Bandera …   Wikipedia Español

  • Fracción continua generalizada — Saltar a navegación, búsqueda En análisis complejo, una rama de las matemáticas, una fracción continua generalizada o fracción fractal es una generalización de una fracción continua en la cual los numeradores parciales y los denominadores… …   Wikipedia Español

  • Infinito — El símbolo de infinito ∞ (Unicode U+221E), también llamado lemniscata, en diferentes fuentes. Para el canal de televisión por cable, véase Infinito (canal de televisión). El concepto de infinito aparece en varias ramas de la filosofía …   Wikipedia Español

  • Oceanía — Para otros usos de este término, véase Oceanía (desambiguación). Oceanía Supe …   Wikipedia Español

  • Inmigración en Chile — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Francia — Para la película de 2010 dirigida por Israel Adrián Caetano, véase Francia (película). «República francesa» redirige aquí. Para otras acepciones, véase República francesa (desambiguación). République française República Francesa …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”