- Producto de Kronecker
-
Producto de Kronecker
En matemáticas, se llama producto de Kronecker, denotado con
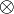 , a una operación sobre dos matrices de tamaño arbitrario que da como resultado una matriz bloque. Es un caso especial del producto tensorial. El producto de Kronecker no debería confundirse con el producto de matrices habitual, que es una operación totalmente diferente. Debe su nombre al matemático alemán Leopold Kronecker.
, a una operación sobre dos matrices de tamaño arbitrario que da como resultado una matriz bloque. Es un caso especial del producto tensorial. El producto de Kronecker no debería confundirse con el producto de matrices habitual, que es una operación totalmente diferente. Debe su nombre al matemático alemán Leopold Kronecker.Contenido
Definición
Si A es una matriz m
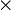 n y B es una una matriz p
n y B es una una matriz p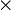 q, entonces el producto de Kronecker A
q, entonces el producto de Kronecker A 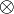 B es la matriz bloque mp
B es la matriz bloque mp nq
nqMás explícitamente, tenemos
Ejemplos
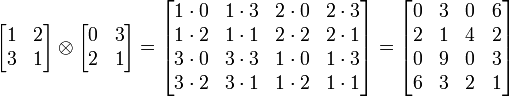 .
.
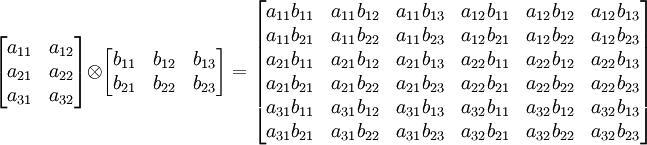 .
.
Propiedades
Bilinealidad y asociatividad
El producto de Kronecker es un caso especial del producto tensorial, así que es bilineal y asociativo
donde A, B y C son matrices y k es un escalar.
El producto de Kronecker no es conmutativo: en general, A
 B y B
B y B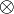 A son matrices diferentes. Sin embargo, A
A son matrices diferentes. Sin embargo, A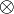 B y B
B y B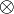 A son equivalentes en permutación, lo que quiere decir que existen matrices permutación P y Q tales que
A son equivalentes en permutación, lo que quiere decir que existen matrices permutación P y Q tales queSi A y B son matrices cuadradas, entonces A
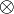 B y B
B y B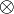 A son incluso de permutación similar, lo que quiere decir que podemos tomar P = QT.
A son incluso de permutación similar, lo que quiere decir que podemos tomar P = QT.La propiedad del producto mixto
Si A, B, C y D son matrices de manera que se puedan formar los productos AC y BD, entonces
A esto se llama la propiedad del producto mixto, porque mezcla el producto ordinario de matrices y el de Kronecker. Se deduce que A
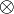 B es inversible si y solo si A y B son inversibles, en cuyo caso la inversa la da
B es inversible si y solo si A y B son inversibles, en cuyo caso la inversa la daEspectro
Supongamos que A y B son matrices cuadradas de tamaños respectivos n y q. Sean λ1,..., λn los autovalores de A y μ1,..., μq los de B (listados de acuerdo a la multiplicidad). Entonces los autovalores de A
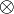 B son
B sonSe deduce que la traza y el determinante de un producto de Kronecker vienen dados por
Valores singulares
Si A y B son matrices rectangulares, entonces se pueden considerar su valores singulares. Supongamos que A tiene rA valores singulares no nulos
De forma similar, denotamos los valores singulares no nulos de B con
Entonces el producto de Kronecker A
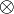 B tiene rArB valores singulares no nulos,
B tiene rArB valores singulares no nulos,Dado que el rango de una matriz es igual al número de sus valores singulares no nulos, encontramos que
Relación con el producto tensorial abstracto
El producto de Kronecker de matrices corresponde al producto tensorial abstracto de aplicaciones lineales. Específicamente, si las matrices A y B representan las transformaciones lineales V1 → W1 y V2 → W2, respectivamente, entonces la matriz A
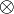 B representa el producto tensorial de las dos aplicaciones, V1
B representa el producto tensorial de las dos aplicaciones, V1 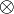 V2 → W1
V2 → W1 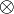 W2.
W2.Ecuaciones matriciales
Se puede usar el producto de Kronecker para obtener una representación conveniente de algunas ecuaciones matriciales. Consideremos por un momento la ecuación AXB = C, donde A, B y C son matrices dadas y X es la incógnita. Podemos reescribir esta ecuación como
Se sigue entonces de las propiedades del producto de Kronecker que la ecuación AXB = C tiene solución única si y sólo si A y B son inversibles.
Aquí, vecX señala el vector formado por los elementos de la matriz X. Específicamente, si X es una matrix m
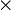 'n', entonces
'n', entoncesHistoria
El producto de Kronecker debe su nombre a Leopold Kronecker, incluso habiendo poca evidencia de que fuera el primero en definirlo y usarlo. De hecho, en el pasado se le llamaba al producto de Kronecker matriz de Zehfuss, por Johann Georg Zehfuss.
Enlaces externos
- Producto de Kronecker en PlanetMath (en inglés)
- MathWorld Matrix: producto directo (en inglés)
Referencia
- Roger Horn and Charles Johnson. Topics in Matrix Analysis, Capítulo 4. Cambridge University Press, 1991. ISBN 0-521-46713-6.
Categorías: Matrices | Álgebra multilineal
Wikimedia foundation. 2010.

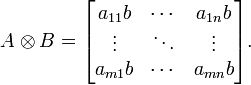
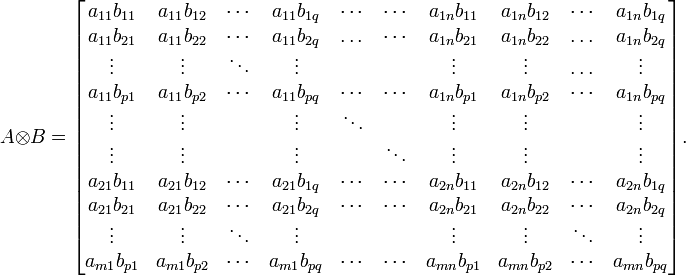
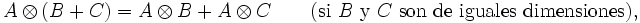
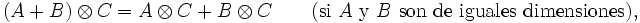
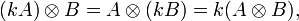
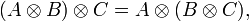
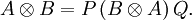
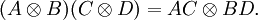
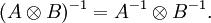
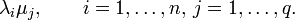
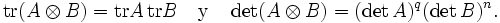
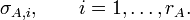
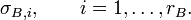
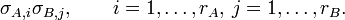
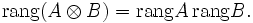
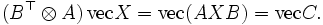
![\operatorname{vec} X = [ x_{11}, x_{21}, \ldots, x_{m1}, x_{12}, x_{22}, \ldots, x_{m2}, \ldots, x_{1n}, x_{2n}, \ldots, x_{mn} ]^\top.](/pictures/eswiki/49/1d9592fc765c94f537f20ad756602683.png)