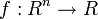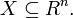En matemáticas, Programación no lineal (PNL) es el proceso de resolución de un sistema de igualdades y desigualdades sujetas a un conjunto de restricciones sobre un conjunto de variables reales desconocidas, con un función objetivo a maximizar, cuando alguna de las restricciones o la función objetivo no son lineales.

Formulación matemática del problema

El problema de programación no lineal puede enunciarse de una forma muy simple:

maximizar una función objetivo

o

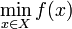minimizar una función objetivo (de coste)

donde

Métodos de resolución del problema

Si la función objetivo f es lineal y el espacio restringido es un politopo, el problema es de Programación lineal y puede resolverse utilizando alguno de los bien conocidos algoritmos de programación lineal.

Si la función objetivo es concava (problema de maximización), o convexa (problema de minimización) y el conjunto de restricciones es convexo, entonces se puede utilizar el método general de Optimización convexa

Existe una variedad de métodos para resolver problemas no convexos. Uno de ellos consiste en utilizar formulaciones especiales de problemas de programación lineal. Otro método implica el uso de técnicas de Ramificación y poda, cuando el problema se divide en subdivisiones a resolver mediante aproximaciones que forman un límite inferior del coste total en cada subdivisión. Mediante subdivisiones sucesivas, se obtendrá una solución cuyo coste es igual o inferior que el mejor limite inferior obtenido por alguna de las soluciones aproximadas. Esta solución es óptima, aunque posiblemente no sea única. El algoritmo puede ser parado antes, con la garantía de que la mejor solución será mejor que la solución encontrada en un porcentaje acotado. Ello se utiliza en concreto en problemas importantes y especialmente difíciles y cuando el problema cuenta con costes inciertos o valores donde la incertidumbre puede ser estimada en un grado de fiabilidad apropiado.

Las condiciones de Karush-Kuhn-Tucker proporcionan las condiciones necesarias para que una solución sea óptima.

Ejemplos

Ejemplo bidimensional

La intersección de la línea con el espacio de restricciones representa la solución

Un problema sencillo puede definirse por las restricciones:

x₁ ≥ 0

x₂ ≥ 0

x₁² + x₂² ≥ 1

x₁² + x₂² ≤ 2

con una función objetivo a ser maximizada

f(x) = x₁ + x₂

donde x = (x₁, x₂)

Ejemplo tridimensional

La intersección de la superfie superior con el espacio de restricciones en el centro representa la solución

Otro problema simple se define por la restricciones:x₁² − x₂² + x₃² ≤ 2

x₁² + x₂² + x₃² ≤ 10

con una función objetivo a ser maximizada

f(x) = x₁x₂ + x₂x₃

donde x = (x₁, x₂, x₃)

Véase también

• Optimización
• Ajuste de curvas
• Método de mínimos cuadrados

Referencias

• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.

• Bazaraa, Mokhtar S. and Shetty, C. M. (1979). Nonlinear programming. Theory and algorithms. John Wiley & Sons. ISBN 0-471-78610-1.

• Nocedal, Jorge and Wright, Stephen J. (1999). Numerical Optimization. Springer. ISBN 0-387-98793-2.

• Bertsekas, Dimitri P. (1999). Nonlinear Programming: 2nd Edition. Athena Scientific. ISBN 1-886529-00-0.

Enlaces externos

• Preguntas frecuentes de programación no lineal (en inglés)
• Glosario de programación matemática (en inglés)
• Nonlinear Programming Survey OR/MS Today

Software

• AIMMS Optimization Modeling AIMMS — Incluye programación no lineal en soluciones sectoriales (prueba gratis, licencia de prueba disponible);
• AMPL solver software - Gratis para estudiantes
• GAMS – Versión gratis disponible para estudiantes