- Punto de acumulación
-
Punto de acumulación
En topología, el concepto de punto de acumulación de un conjunto en un espacio captura la noción de estar extremadamente cercano al conjunto sin pertenecer necesariamente a él. Generaliza la noción de límite en
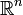.También se utiliza como sinónimo: punto límite.
Contenido
Definición
Dado un conjunto E y un punto p en un espacio métrico X, decimos que él es un punto de acumulación para E, si cualquier ε-vecindad de p sin p, tiene intersección no vacía con E. Es decir, hay elementos de E que están ε-cercanos a p y son diferentes de p mismo (dicha restricción no aparece cuando se trata de puntos de adherencia). En esta definición podemos ver que p puede o no estar en E.
Es posible generalizar el concepto a espacios topológicos reemplazando las ε-vecindades con conjuntos abiertos.
Con símbolos
Se denota con E' al conjunto de puntos límite de E, podemos definir conforme a:
-
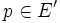si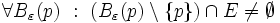 
Ejemplo
El intervalo (0,1) tiene como puntos de acumulación al intervalo [0,1].
Un conjunto finito no tiene puntos de acumulación (hay que tener en cuenta que siempre hablamos de números reales (o complejos, o incluso de racionales en un intervalo en el que sepamos con seguridad que no hay irracionales), pues no tendría sentido hablar del concepto "infinitamente próximo" con los números enteros por ejemplo.
El conjunto de puntos de acumulación en Q es igual al de R, ya que Q es denso en R.
N no tiene punto de acumulación. Por lo tanto, cada punto en N es aislado.
Caracterización de conjuntos cerrados
- Teorema:
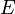es un conjunto cerrado si 
.
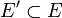Válido en espacios métricos y topológicos. Y valido en cualquier espacio.
Otras consecuencias
Sea E un subconjunto cualquiera en un espacio topológico, entonces tenemos
-
- Si 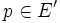entonces hay una sucesión
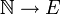la cual converge a p
- Si
Podemos interpretar esto como que para cada elemento de
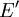, el conjunto derivado de E (así también se le nombra al conjunto de los puntos de acumulación) existen elementos del espacio que forman una sucesión convergente dentro de E aunque el punto ni siquiera este en él.La demostración de esta proposición es bastante natural.
Referencia
W. Rudin. Principles of Mathematical Analysis. McGraw-Hill, 1976. ISBN 0-07-054235-X
Categorías: Análisis matemático | Topología -
Wikimedia foundation. 2010.
