- Espacio métrico
-
Espacio métrico
En matemática, un espacio métrico es un tipo particular de espacio topológico donde una distancia entre puntos está definida. Corresponde al caso muy común en que se dispone de una noción de distancia sobre el espacio.
Definiciones
Definición de espacio métrico
Formalmente, un espacio métrico es un conjunto M (a cuyos elementos se les denomina puntos) con una función distancia asociada (también llamada una métrica)
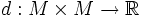(donde R es el conjunto de los números reales). Para todo x, y, z en M, esta función debe satisfacer las siguientes condiciones:- d(x, y) ≥ 0
- d(x, x) = 0 (reflexividad)
- si d(x, y) = 0 entonces x = y (identidad de los indiscernibles)
- d(x, y) = d(y, x) (simetría)
- d(x, z) ≤ d(x, y) + d(y, z) (desigualdad triangular).
Otras definiciones
- Se llama bola (abierta) centrada en
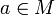y de radio 
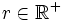, al conjunto 
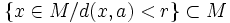. Se denota usualmente como 
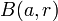. - Se llama bola cerrada centrada en 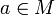y de radio 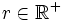, al conjunto
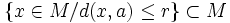. Se denota usualmente como 
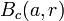o por 
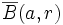. - En análisis funcional la terminología puede llevar un poco a confusión, pues a la bola abierta de radio
y centro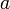 
se la suele denotar 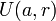por 
o por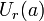 
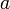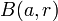, mientras -y aquí viene la posible confusión- a la bola cerrada de centro y radio se la denota por o por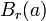 
. - Algunos autores utilizan la expresión disco en lugar de bola, así es que se puede hablar en términos de disco abierto y disco cerrado. En particular, esta terminología se utiliza en Variable Compleja, y cuando se considera la distancia euclídea sobre el conjunto
.
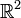Topología de un espacio métrico
La distancia dota a M de una topología, definiendo un subconjunto o parte U como abierta cuando:
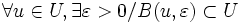. A dicha topología se la denomina topología inducida por d en M.Podemos entonces interpretar intuitivamente que un conjunto abierto es entonces una parte que tiene un cierto "espesor" alrededor de cada uno de sus puntos.
Un subespacio métrico
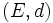de un espacio métrico 
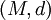es subespacio topológico del espacio topológico 
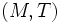, donde 
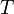es la topología en 
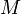inducida por d. Es decir, 
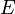hereda de 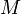la topología inducida por d.Un entorno V de un punto a de un espacio métrico M no es más que un subconjunto
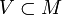de forma que exista un r > 0 tal que la bola abierta 
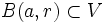. El conjunto 
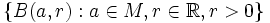es base de la topología inducida por d, y también es base de entornos de dicha topología. Como 
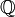es denso en 
, resulta entonces que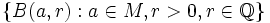 
también es base de entornos de la topología inducida por d. En consecuencia, todo espacio métrico cumple el Primer Axioma de Numerabilidad.Todo espacio métrico es espacio de Hausdorff. Además, al igual que ocurre en espacios pseudométricos, para los espacios métricos son equivalentes las siguientes propiedades: ser espacio de Lindelöf, cumplir el Primer Axioma de Numerabilidad y ser separable.
Sistemas axiomáticos alternativos
La propiedad 1 (d(x, y) ≥ 0) se sigue de la 4 y la 5. Algunos autores usan la recta real extendida y admiten que la distancia tome el valor ∞. Cualquier métrica tal puede ser reescalada a una métrica finita (usando d'(x, y) = d(x, y) / (1 + d(x, y)) o d''(x, y) = min(1, d(x, y))) y los dos conceptos de espacio métrico son equivalentes en lo que a topología se refiere. Una métrica es llamada ultramétrica si satisface la siguiente versión, más fuerte, de la desigualdad triangular.
-
.
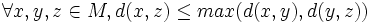Si se elimina la propiedad 3, se obtiene un espacio pseudométrico. Sacando, en cambio, la propiedad 4, se obtiene un espacio quasimétrico. No obstante, perdiéndose simetría en este caso, se cambia, usualmente, la propiedad 3 tal que ambas d(x,y)=0 y d(y,x)=0 son necesarias para que x y y se identifiquen. Todas las combinaciones de lo anterior son posibles y referidas por sus nomenclaturas respectivas (por ejemplo como quasi-pseudo-ultramétrico).
Ejemplos
- La distancia trivial: d(x,y) = 0 si x = y, caso contrario, 1.
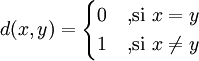
- Los números reales con la función distancia d(x, y) = |y - x| dada por el valor absoluto, y más generalmente n-espacio euclídeo con la distancia euclídea, son espacios métricos completos.
- Más generalmente aun, cualquier espacio vectorial normado es un espacio métrico definiendo d(x, y) = ||y - x||. Si tal espacio es completo, lo llamamos espacio de Banach.
- Si X es un conjunto y M es un espacio métrico, entonces el conjunto de todas las funciones acotadas f : X -> M (i.e. aquellas funciones cuya imagen es un subconjunto acotado de M) puede ser convertido en un espacio métrico definiendo d(f, g) = supx en X d(f(x), g(x)) para cualesquiera funciones acotadas f y g. Si M es completo, entonces este espacio es completo también.
- Si X es un espacio topológico y M es un espacio métrico, entonces el conjunto de todas las funciones continuas acotadas de X a M forma un espacio métrico si definimos la métrica como antes: d(f, g) = supx en X d(f(x), g(x)) para cualesquiera funciones continuas acotadas f y g. Si M es completo, entonces este espacio es completo también.
- Si M es un espacio métrico, podemos convertir al conjunto K(M) de todos los subconjuntos compactos de M en un espacio métrico definiendo distancia de Hausdorff d(X, Y) = inf{r: para cada x en X existe un y en Y con d(x, y) < r y para cada y en Y existe un x en X con d(x, y) < r). En este métrica, dos elementos están cerca uno de otro si cada elemento de un conjunto está cerca de un cierto elemento del otro conjunto. Se puede demostrar que K(M) es completo si M es completo.
Un análisis lógico
- El concepto métrico fundamental es el de función corta, los morfismos de la categoría métrica (los isomorfismos, i.e. aplicaciones bi-cortas, son las isometrías), pero su expresión usual usa el orden y la suma en los reales positivos luego,
- 1) Es obvio que : | x - |x - y | | = y es lo mismo que x = 0 o y ≤ x, luego distancia en los reales positivos da orden débil allí, orden fuerte (y ≤ x ssi ... ) es difícil, pero posible, si se acepta una solución de |x - y | = y i.e. y = x / 2.
- 2) | d(y, z) - |d(y, z) - d´(f(y), f(z)) | | = d´(f(y), f(z)) expresa que f es una función corta, sin ninguna referencia a un orden en los reales positivos.
- 3) La siguiente equivalencia de la desigualdad triangular
- | d(x, y) - d(x, z) | ≤ d(y, z)
expresa (sin ninguna referencia a una operación en los reales positivos, |x - y| es la distancia allí) el hecho que d(x, -) es función corta (luego uniforme, luego continua). d: x - > d(x,-) es una isometría.
- Reuniendo ambas : | d(y, z) - |d(y, z) - | d(x, y) - d(x, z) | | | = | d(x, y) - d(x, z) | expresa desigualdad triangular directamente.
- un leve cambio : | d(y, z) - |d(z, y) - | d(x, y) - d(x, z) | | | = | d(x, y) - d(x, z) | expresa desigualdad triangular y simetría (hacer z = x y usar | x - d(y, y)| = x).
Espacios metrizables.
Un espacio topológico (X,T) se dice que es metrizable cuando existe una distancia d cuya topología inducida sea precisamente la topología T.
Un problema fundamental en Topología es determinar si un espacio topológico dado es o no metrizable. Existen diversos resultados al respecto.
Teorema de metrización de Urysohn.
Todo espacio topológico regular que cumpla el Segundo Axioma de Numerabilidad es metrizable.
Teorema de metrización de Nagata-Smirnov (condición suficiente).
Todo espacio regular con una base numerable localmente finita es metrizable.
Teorema de metrización de Nagata-Smirnov (condición suficiente).
Todo espacio metrizable tiene una base numerable localmente finita.
Teorema de metrización de Stone.
Todo espacio metrizable es paracompacto.
Teorema de metrización de Smirnov.
Un espacio topológico es metrizable si y solo si es paracompacto y localmente metrizable.
Teorema de metrización de espacios completamente separables.
Un espacio topológico completamente separable es metrizable si y solo si es regular.
Véase también
- topología
- desigualdad triangular
- Lipschitz continua
- isometría, contracción y función corta
- Categoría de los espacios métricos
Categorías: Topología | Geometría métrica
Wikimedia foundation. 2010.
